Acest capitol are ca obiect de studiu calculul unor corpuri solide ce au toate dimensiunile de acelaşi ordin de mărime, adică se încadrează în categoria corpurilor masive. Solicitările lor mecanice (dar şi cele termice, care nu sunt abordate aici) produc în volumul pieselor tensiuni care variază în mod semnificativ pe grosimea pereţilor, iar caracterizarea acestei variaţii este una dintre ţintele calculelor inginereşti aplicate acestor corpuri.

Fig. 10.1

            Tuturor le este comună simetria axială a construcţiei, a solicitărilor şi a efectelor pe care acestea le produc (însemnând că efectele sunt aceleaşi în toate punctele aflate la aceeaşi rază r, dintr-o secţiune transversală oarecare), ceea ce simplifică în mod hotărâtor condiţiile de calcul, care altfel ar fi extrem de complicate.

Tuburi cu pereţi groşi

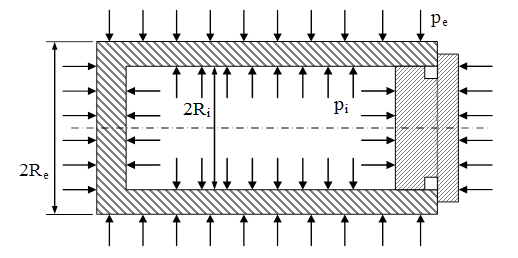
Se consideră că fac parte din această clasă corpurile tubulare pentru care grosimea pereţilor (Re - Ri) are mărimea de cel puţin o cincime din raza lor interioară Ri. Lungimea acestor corpuri nu este importantă pentru calculul tensiunilor, întrucât în principiu acestea evoluează la fel în toate secţiunile transversale, atunci când încărcările lor sunt date de presiunea interioară pi, respectiv de cea exterioară pe, ca în figura de mai jos.
Schema din figură prezintă situaţia cea mai generală, a unui tub închis la capete prin capace, la care în pereţi apare o categorie specifică de tensiuni, având direcţie longitudinală, notate prin σx şi calculate prin raportarea efectelor rezultante, de tip forţă, ale celor două feluri de presiuni, la aria de material din secţiunile transversale, astfel:
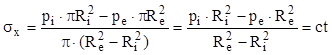                (10.1)

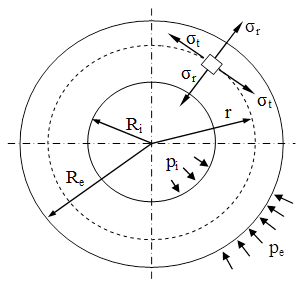Fig. 10.2

Se observă că aceste tensiuni au mărime constantă pe lungimea tubului, adică sunt constante în toate punctele din pereţii acestui corp. În plus, ele sunt de întindere, dacă tubul este solicitat numai de presiunea interioară, dar de comprimare, dacă presarea se produce numai din exterior.
Schema alăturată prezintă modul în care apar celelalte două categorii de tensiuni importante în calculul tuburilor; dirijate radial, respectiv circumferenţial, ele sunt reprezentate pe elementul de volum aflat la raza r în peretele tubului studiat.
Tensiunile notate cu σr, σt şi σx (dacă există) reprezintă valorile principale ale stării de tensiuni din pereţii tubului, care este spaţială, în tuburile închise la capete prin capace şi plană, dacă acestea lipsesc, .
După cum s-a arătat, solicitarea tubului este axial-simetrică, deci valorile tensiunilor depind, pe secţiunile transversale, numai de raza r, fiind constante în toate punctele aflate la aceeaşi distanţă de axa longitudinală.
Se demonstrează că această dependenţă este de tip hiperbolic, iar relaţiile de calcul pot fi scrise într-o formă unificată, astfel:
                   (10.2)
Este interesant de remarcat că prima fracţie din această expresie reprezintă mărimea constantă a tensiunii longitudinale σx, iar forma expresiei arată că această valoare este media aritmetică a celorlalte două tensiuni principale:
                                (10.3)
Din acest motiv, tensiunea σx este mai puţin importantă în calculele de rezistenţă, mai ales dacă se folosesc teoriile de rupere bazate pe valorile extreme ale tensiunilor principale (aşa cum sunt teoriile σmax şi τmax).
Variaţia tensiunilor radiale şi circumferenţiale pe grosimea pereţilor se analizează separat, pentru cele două categorii mari de solicitări.

A. Tuburi solicitate numai de presiuni exterioare

Relaţiile pentru calculul tensiunilor din secţiunile transversale se obţin (sub formă unificată) înlocuind în (10.2) pi = 0:
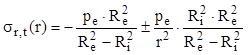                     (10.4)
Pe baza acestor expresii este interesant de remarcat că, în cazurile în care Ri=0 (piese pline, de tip arbore, presate din exterior), se obţine σr = σt = -pe , adică tensiunile nu mai depind de raza r şi sunt egale între ele în orice punct din pereţii piesei studiate.
Pentru a observa evoluţia tensiunilor, atunci când raza punctului de calcul creşte de la Ri la Re se scriu, pe rând, relaţiile celor două categorii de tensiuni şi se studiază funcţiile astfel obţinute.

a) Tensiunile radiale

Legea de variaţie se scrie:
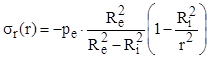   (10.5)
Termenul al doilea din paranteză este subunitar şi scade mereu, atunci când punctul de calcul parcurge grosimea peretelui de la interior către exterior; valoarea parantezei creşte şi ea, fiind pozitivă pe toată grosimea, încât valorile tensiunii sunt peste tot negative. Variaţia lor este de tip hiperbolic, iar valorile la capetele diagramei sunt:

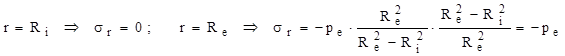
b) Tensiunile circumferenţiale

Funcţia lor de raza r este următoarea:
                          (10.6)
Evoluţia este descrescătoare, iar valorile de la capete sunt:

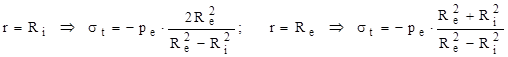
Din graficele de variaţie trasate pentru cele două categorii de tensiuni (fig. 10.3) se observă că solicitarea periculoasă a tubului se produce la interior, unde starea de tensiuni este de comprimare monoaxială (componentele radiale sunt nule) şi deci relaţia calculului de rezistenţă (în care se foloseşte rezistenţa admisibilă la compresiune σac a materialului tubului) se scrie:
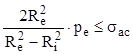                                (10.7)
De obicei din această relaţie se obţine valoarea necesară a razei exterioare Re, cunoscând ceilalţi parametri, pe baza unor operaţii matematice simple:
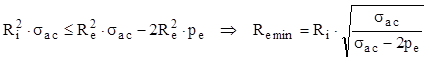         (10.8)
Aspectul acestei relaţii arată că există valori de presiune pe care un astfel de tub nu le poate prelua, indiferent cât de mult s-ar creşte grosimea pereţilor săi. Astfel, din condiţia ca numitorul fracţiei de sub radical să fie pozitiv rezultă o limitare importantă a presiunilor exterioare suportate de tuburile cu pereţi groşi, care trebuie să fie mai mici cu cel puţin 50% faţă de rezistenţa admisibilă la compresiune a materialului din care sunt făcute!

B. Tuburi solicitate numai de presiuni interioare

Relaţiile pentru calculul tensiunilor se obţin înlocuind în (10.2) pe = 0:
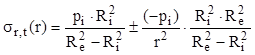                    (10.9)

a) Tensiunile radiale

Legea de variaţie se scrie:
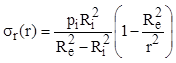 (10.10)
Ultima fracţie este mai mare decât unitatea, iar diferenţa din paranteză este negativă şi scade mereu, când raza creşte de la interior către exterior; încât valorile tensiunii sunt descrescătoare şi peste tot negative. Variaţia lor este de tip hiperbolic, iar valorile din punctele de la capetele diagramei sunt:

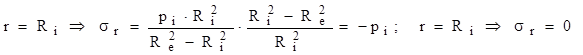
b) Tensiunile circumferenţiale

Funcţia lor de raza r este următoarea:
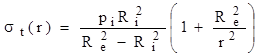                     (10.11)
Se poate observa că paranteza este pozitivă descrescătoare, la fel ca şi evoluţia tensiunilor, iar valorile de la capete sunt:

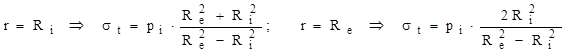
Din graficele de variaţie ale celor două categorii de tensiuni (fig. 10.4) se observă că solicitarea periculoasă a tubului se produce la interior, unde starea de tensiuni este plană (respectiv spaţială, în tuburile închise la capete, la care s-a arătat că tensiunea longitudinală este cât media valorilor celorlalte două), cu tensiunile principale având semne contrare; în astfel de cazuri este util să se calculeze efectul lor global folosind ipoteza de rupere τmax, iar relaţia calculului de rezistenţă se obţine astfel:
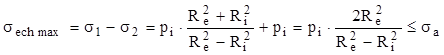         (10.12)
Se observă asemănarea acesteia cu expresia similară (10.7) de la tuburile cu presiune exterioară, încât valoarea necesară a razei exterioare Re va avea practic aceeaşi formulă de calcul ca mai sus:
                              (10.13)
Şi pentru tuburile cu presiuni interioare se constată că nu pot prelua valori de presiune oricât de mari, întrucât acestea trebuie să fie mai mici cu cel puţin 50% faţă de rezistenţa admisibilă a materialului din care sunt făcute!

Tuburi fretate

Există mai multe metode prin care să poată fi extins intervalul de presiuni interioare pe care un tub cu pereţi groşi le poate suporta; principiul de bază constă în aplicarea la exteriorul tubului a unei solicitări de comprimare (operaţie denumită pretensionare), astfel încât să se modifice în mod convenabil repartiţia tensiunilor în pereţii corpului studiat.
Comprimarea exterioară poate fi realizată, de exemplu, prin înfăşurarea (bobinarea) strânsă a unui cablu de oţel, dar cel mai des se aplică operaţia de fretare: tubul care trebuie tratat se introduce în interiorul altui tub cu pereţi groşi, care are diametrul interior ceva mai mic (cu diferenţe maxime de ordinul zecimilor de milimetri) faţă de cota exterioară a tubului iniţial. Această îmbinare cu strângere se obţine prin presare, sau aducând la temperaturi ridicate tubul exterior pentru a se dilata înainte de montare.

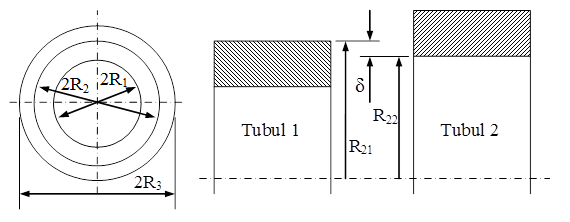Fig. 10.5

            Diferenţa dintre razele de montare R2 ale celor două tuburi (fig. 10.5), notată de obicei cu δ, este numită „strângere de fretare” şi este parte într-o relaţie de dependenţă cu presiunea de fretare p0, în care mai apar razele interioare şi exterioare ale celor două tuburi, dar şi caracteristicile elastice (modulul lui Young şi coeficientul lui Poisson) ale materialelor din care sunt fabricate:
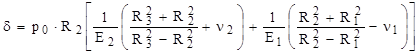          (10.14)
Se observă că, dacă ambele tuburi sunt din acelaşi material, atunci relaţia se simplifică foarte mult:
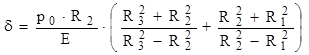                     (10.15)
Aceste relaţii se folosesc, de obicei, pentru a stabili presiunea care ia naştere între cele două tuburi, pentru o valoare dată a strângerii de fretare, atunci când celelalte mărimi din aceste relaţii sunt cunoscute. De exemplu, pentru cazul tuburilor din acelaşi material, din relaţia (10.15) se obţine următoarea expresie a presiunii de fretare:
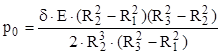                          (10.16)
După ce se calculează această valoare este interesant să fie urmărită, după modelul analizelor de mai sus, influenţa presiunii suplimentare asupra distribuţiei de tensiuni în pereţii celor două tuburi. În acest scop, se trasează mai întâi diagramele tensiunilor principale determinate (în tubul compus, considerat global) de acţiunea presiunii interioare pi, pe care este desemnat să o preia tubul interior. Se studiază apoi tensiunile produse de presiunea de fretare p0, care acţionează ca presiune exterioară în tubul iniţial 1, respectiv interioară pentru tubul suplimentar 2. În final, se trasează diagramele pentru cele două categorii de tensiuni rezultante din pereţii tuburilor.

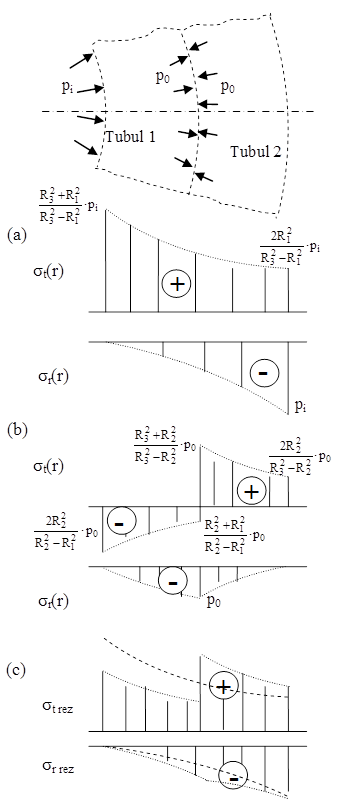Fig. 10.6

   Figura alăturată prezintă, în ordinea precizată mai sus, cele trei feluri de diagrame pentru tensiunile din pereţii tubului compus studiat.
De pe graficele tensiunilor rezultante se poate observa că prin comprimarea exterioară a tubului iniţial se obţine un efect favorabil – micşorarea tensiunii periculoase σt(R1), dar şi un efect negativ, produs prin creşterea importantă a tensiunii circumferenţiale la interiorul tubului suplimentar.
Această tensiune este de obicei mai mică decât valoarea iniţială σt(R1), dat trebuie observat că starea periculoasă de solicitare se produce la interiorul tubului 2 şi acolo se face calculul de rezistenţă.
O discuţie importantă este legată de optimizarea unei astfel de îmbinări: alegând în mod convenabil mărimea δ a strângerii de fretare, se poate ajunge la acelaşi nivel de solicitare maximă în cele două tuburi utilizate.
Astfel, folosind ipoteza de rupere τmax şi egalând valorile tensiunilor echivalente din punctele cele mai solicitate ale tuburilor (admise a fi fabricate din acelaşi material), se obţine o relaţie pentru δoptim, astfel:
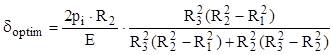                (10.17)
Cu această valoare se poate calcula σech max din cele două tuburi, iar dacă se derivează în raport cu raza de graniţă R2 expresia astfel obţinută şi se egalează cu zero rezultatul se găseşte că în tubul global obţinut prin fretare solicitarea rezultantă va fi minimă (şi la fel de periculoasă în cele două tuburi) dacă raza comună a tuburilor componente va avea valoarea:
                               (10.18)
Pe baza acestui rezultat se poate calcula tensiunea echivalentă maximă din tuburi, reprezentând cea mai mică valoare posibilă a acestei mărimi:
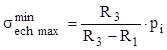                          (10.19)
Pe de altă parte, introducând valoarea optimă a razei comune în relaţia (10.17) se calculează strângerea optimă care îi corespunde; pentru început, este suficient să se aducă la o formă mai simplă ultima fracţie din relaţia respectivă, astfel:

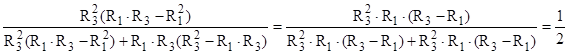
Rezultă că strângerea optimă ce trebuie folosită la fretare va fi:
                            (10.20)
Expresiile (10.17) – (10.20) sunt cunoscute ca relaţiile lui Gadolin şi stau la baza calculelor de optimizare pentru tuburile îmbinate prin fretare. Se poate demonstra că fretarea este avantajoasă numai pentru tuburile care au raza interioară R1 mult mai mică decât cea exterioară R3.
Mai trebuie precizat că, deoarece toate relaţiile de calcul de mai sus se demonstrează pe baza proprietăţilor elastice ale materialelor şi a regulilor din teoria elasticităţii, ele sunt valabile numai dacă în tot volumul tubului calculat tensiunile au valori care nu depăşesc limita de proporţionalitate a materialului folosit. În caz contrar, calculul tuburilor va conduce la alte rezultate, întrucât trebuie făcut pe baza teoriei plasticităţii.

Discuri (de grosimi mici şi uniforme) în mişcare de rotaţie

Calculul acestor corpuri masive se face după aceleaşi principii ca la tuburile cu pereţi groşi, cu diferenţa importantă că solicitarea exterioară este dată de forţele centrifuge produse prin rotirea corpului considerat, cu viteza unghiulară constantă ω,în jurul axei sale longitudinale de simetrie. Forma discurilor este cilindrică scurtă, înălţimea cilindrului fiind numită grosimea h a discului, de valoare constantă şi relativ mică faţă de diametrul exterior al corpului (De = 2Re). Cilindrul are de obicei un gol la interior, tot cilindric, de diametru relativ mic (Di = 2Ri), necesar pentru ca discul să fie montat pe axul care îl va antrena în rotaţie. Pentru calcule sunt importante şi greutatea specifică γ, respectiv densitatea ρ = γ/g ale materialului din care este făcut discul care trebuie studiat.
Este important de observat că, datorită valorii mici a lui h, tensiunile care apar în material nu variază pe grosimea discului; în plus, componentele lor care acţionează paralel cu axa de rotaţie (σx) pot fi considerate egale cu zero. Prin urmare, în orice punct din volumul unui astfel de disc solicitarea prin forţele centrifuge va produce o stare plană de tensiuni.
Studiind echilibrul dinamic al unui volum elementar plasat la raza r faţă de axa de rotaţie şi exprimând apoi tensiunile în funcţie de deformaţiile specifice în ecuaţia diferenţială astfel obţinută, se ajunge la expresiile tensiunilor principale în funcţie de două constante de integrare; valorile lor se calculează din condiţiile la limită (σr=0 pe suprafeţele libere ale discului, unde nu există presiuni), iar relaţiile după care tensiunile principale variază cu raza de poziţie r se scriu astfel:
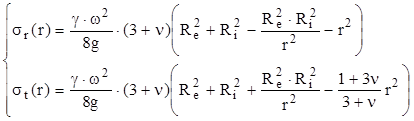                (10.21)

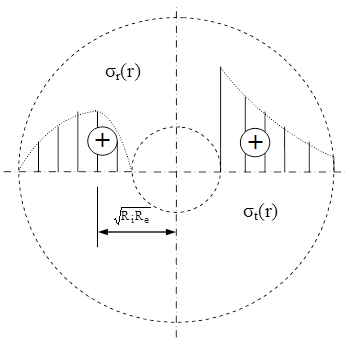Fig. 10.7

Se observă că dependenţa de rază are o formă mai complexă decât în cazul tuburilor cu pereţi groşi.
Pentru tensiunile radiale se obţine că valorile de la capetele intervalului de variaţie sunt egale cu zero, iar anularea derivatei expresiei σr(t) duce la aflarea poziţiei r0 din punctul de extrem:
Înlocuind această valoare în expresia tensiunilor radiale, se obţine valoarea lor maximă:

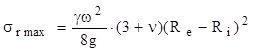
Funcţia tensiunilor circumferenţiale este strict descrescătoare şi înlocuind valorile razelor de la capetele intervalului de definiţie se obţin, după efectuarea unor transformări relativ simple, următoarele expresii:

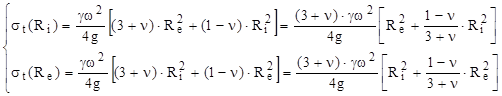
Diagramele din figura 10.7 arată că solicitarea periculoasă se produce la interiorul discului, unde starea de tensiuni este uniaxială, astfel încât relaţia calculului de rezistenţă pentru un astfel de disc se scrie:
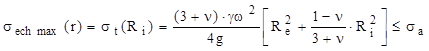         (10.22)
Pentru discurile compacte, fără gaură la interior, calculul tensiunilor se bazează tot pe relaţiile (10.21), făcând Ri = 0, de unde rezultă:
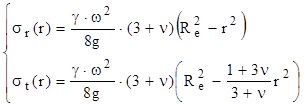              (10.23)

Fig. 10.8

Se observă că ambele legi de variaţie sunt descrescătoare cu raza de poziţie r (fig. 10.8), iar valorile lor maxime, care se obţin în centrul discului (la r=0), sunt egale între ele, astfel:

Tensiunile radiale sunt şi în acest caz nule la capetele intervalului, în vreme ce făcând calculele se obţine că tensiunile σt(r) au la raza exterioară valoarea:

Solicitarea periculoasă are loc în centrul discului, unde tensiunile au aceeaşi valoare în toate direcţiile, astfel încât folosind prima ipoteză de rupere relaţia calculului de rezistenţă este:
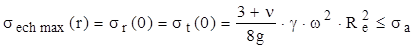               (10.24)
Exemplu de calcul: se consideră un disc de oţel, având greutatea specifică γ=78×10-6N/mm3, rezistenţa admisibilă σa=160MPa şi coeficientul de contracţie transversală ν=0,3. Să se stabilească turaţia maximă pe care discul o poate suporta, ştiind că este construit plin, adică nu are gaură centrală, iar diametrul lui este D=0,6m.
Din relaţia (10.24) se calculează viteza unghiulară admisibilă:

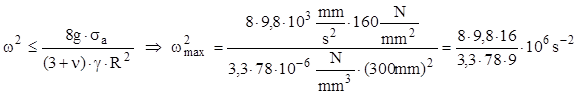
Făcând calculele se obţine ωmax = 736rad/s. Turaţia maximă permisă se obţine dintr-o relaţie cunoscută din mecanică:

Discul calculat suportă turaţii destul de mari, de până la 7000 ture/min.

Aplicaţii

În cele ce urmează vor fi abordate cele mai importante aspecte legate de calculul corpurilor masive abordate mai sus, aşa cum sunt întâlnite în practica inginerească. Acolo unde va fi cazul se va face apel la relaţiile şi figurile prezentate în acest capitol, fără a se relua explicaţiile date anterior.

10.1. Se proiectează o presă hidraulică, având capacitatea Fmax = 250tf; se cere să se dimensioneze cilindrul acestei prese, ştiind că diametrul său interior este Di=400mm şi că materialul din care este făcut are σa=100MPa.

Rezolvare

Cilindrul presei este un tub cu pereţi groşi, solicitat de presiunea interioară de lucru, a cărei valoare maximă trebuie calulată pe baza forţei pe care trebuie să o dezvolte presa, astfel:

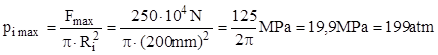
Se observă că tuburile de acest fel trebuie să suporte presiuni ridicate, cu un ordin de mărime mai mari decât cele întâlnite la vasele cu pereţi subţiri. Pe aceasta se bazează necesitatea grosimilor mari ale pereţilor.
Dimensionarea cilindrului înseamnă stabilirea valorii minime a razei sale exterioare, folosind relaţia (10.13) stabilită mai sus:

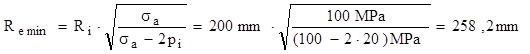
Se adoptă valoarea Re ad = 260mm, deci cilindrul va avea De = 520mm.

10.2. Să se stabilească strângerea maximă cu care un inel de oţel, având σa=180MPa, E=21×104MPa, lăţimea L=40mm şi diametrele Di=100mm, De=120mm, poate fi montat pe un arbore din acelaşi material. Dacă se admite între cele două piese coeficientul de frecare μ=0,2 să se calculeze ce forţă de apăsare Fmin este necesară, la această strângere maximă, pentru montarea sau demontarea prin presare a inelului pe sau de pe arbore.

Rezolvare

Ideea de bază pentru calculul acestei îmbinări este că se are în vedere fretarea inelului pe un tub cu formă particulară, în sensul că este plin, adică diametrul său interior este nul, ceea ce înseamnă că în relaţiile prezentate anterior vom avea R1=0.
Înainte de a calcula strângerea admisibilă, cu formulele de la tuburile fretate făcute din acelaşi material, trebuie stabilită presiunea interioară maximă pe care inelul considerat o poate suporta, din condiţia de rezistenţă (10.12), bazată pe ipoteza de rupere τmax:

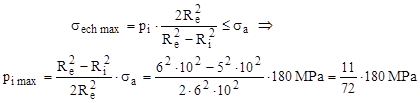
Acest rezultat nu este unul final, deci poate fi folosit în calcule ulterioare sub această formă. Strângerea maximă permisă va fi calculată direct, folosind relaţia (10.15) a tuburilor fretate:

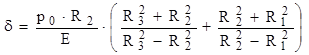
Folosind datele problemei relaţia devine:

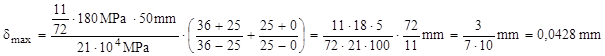
Pentru ca inelul să reziste operaţiei de montare, diametrul arborelui poate fi mai mare decât diametrul interior al inelului cu cel mult 85μm.
Forţa de apăsare pentru introducerea sau scoaterea inelului pe arbore trebuie să învingă (adică să fie măcar cu 10% mai mare decât) forţa de frecare Ff dintre cele două piese, care la rândul ei depinde de forţa normală de presare Nf de pe suprafaţa cilindrică, de diametru Di şi înălţime L, pe care se produce contactul dintre inel şi arbore:

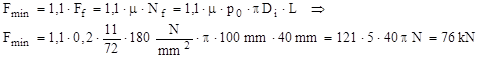
Prin urmare, montarea sau demontarea inelului prin presare la rece necesită forţe apreciabile, deci trebuie să se bazeze pe prese de capacitate mare. Din acest motiv este interesant de văzut în ce condiţii s-ar putea executa pe altă cale operaţia de fretare, adică prin încălzirea inelului, pentru a i se creşte diametrul prin dilatare termică.
Considerând că temperatura va fi crescută cu ΔT şi luând valoarea uzuală, pentru oţelurile obişnuite, a coeficientului de dilatare liniară α=1,2×10-5grd-1, se aplică relaţia clasică cu care se calculează valoarea dilatărilor liniare, ΔD = α×Di×ΔT, din care folosind valoarea strângerii maxime de mai sus se poate obţine diferenţa de temperatură necesară:

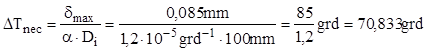
Operaţia de montare se poate face şi prin încălzirea prealabilă a inelului cu o diferenţă de temperatură de cel puţin 71°C; în funcţie de dotările tehnologice de care se dispune, este probabil că această metodă va fi preferată, în locul celei de presare la rece.

10.3. Se proiectează un tub cu pereţi groşi, care să preia o presiune interioară pi=150MPa, deşi materialul avut la dispoziţie este un oţel cu rezistenţa admisibilă de doar 250MPa. Este nevoie de un tub compus, cu îmbinare prin fretare, iar diametrul interior trebuie să fie Di=2R1=300mm; să se stabilească valorile potrivite ale razelor R2, R3 şi strângerii δ, pentru ca tubul să funcţioneze în cele mai bune condiţii posibile.

Rezolvare

Calculul optimizat al îmbinării se bazează pe relaţiile (10.18) – (10.20), ale lui Gadolin. Mai întâi se poate stabili raza exterioară a tubului global, folosind formula (10.19) a tensiunii echivalente optimizate:

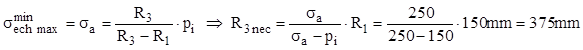
Se calculează apoi raza comună optimă a celor două tuburi componente, cu formula (10.18) de mai sus:

Cu această valoare, înlocuită în relaţia (10.20), se determină strângerea optimă de fretare pentru montarea celor două tuburi:

Tubul suplimentar trebuie să aibă diametrul interior mai mic cu 0,338mm faţă de cota exterioară a tubului de bază.
Dacă îmbinarea se realizează prin încălzirea tubului exterior, atunci diferenţa de temperatură cu care acesta trebuie încălzit se calculează pe principiile discutate la aplicaţia 10.2, astfel:

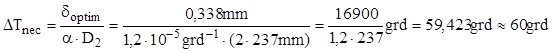
Pentru efectuarea corectă a montării, tubul suplimentar trebuie încălzit cu cel puţin 60°C.

10.4. O roată de curea cu diametrul D = 400mm şi lăţimea L = 100mm se montează prin presare pe un arbore de transmisie având secţiunea circulară plină cu diametrul d = 100mm. Ambele piese sunt din oţel cu modulul de elasticitate E = 21×104MPa, coeficientul de frecare pe suprafeţele de contact fiind μ = 0,1. Roata trebuie să transmită către arbore, cu un coeficient de siguranţă c = 2, momentul dezvoltat de motorul de antrenare având drept caracteristici nominale turaţia n = 750 ture/minut şi puterea P = 300kW.
Să se calculeze strângerea de fretare necesară pentru realizarea, în condiţiile date, a acestei îmbinări, ca şi forţa minimă de presare pentru montarea, respectiv demontarea celor două piese.
Rezolvare

Există mai multe aspecte de bază în analiza acestei teme de proiectare. Mai întâi, trebuie clarificat înţelesul noţiunii de coeficient de siguranţă în buna funcţionare a unei transmisii de mişcare şi putere: practic, este necesar ca îmbinarea care va fi calculată să poată prelua un moment de c ori mai mare decât momentul dezvoltat de motorul de acţionare.
Folosind cunoştinţele de la studiul solicitărilor simple, privind legătura între caracteristicile de fabricaţie ale motorului şi momentul de răsucire pe care acesta îl transmite, se poate calcula momentul capabil necesar pentru îmbinarea proiectată, astfel:

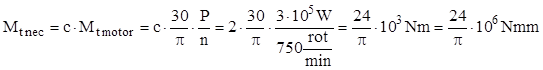
Momentul pe care îmbinarea îl transmite se stabileşte pe baza rezultantei forţelor de frecare dezvoltate la contactul dintre arbore şi roată, care se calculează aşa cum a fost explicat la aplicaţia 10.2; momentul acestei rezultante în raport cu axa longitudinală a arborelui este:

Cele două rezultate de mai sus trebuie să fie egale între ele:

Strângerea de fretare necesară se obţine din relaţia (10.15):

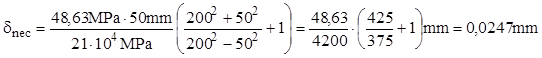
Diametrul arborelui trebuie să fie cu 50μm mai mare decât diametrul interior al roţii. În aceste condiţii, forţa minimă de presare pentru montarea sau demontarea roţii va fi: