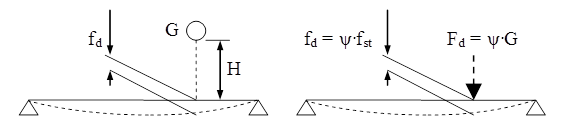Capitolele anterioare, inclusiv cele privind solicitările simple, au avut ca obiect de studiu încărcările aplicate static, adică lent şi cu variaţii neglijabile ale intensităţii sarcinilor exterioare. În cele ce urmează vor fi abordate principiile de bază ale calculelor în cazul corpurilor solide care sunt solicitate dinamic, fie prin aplicarea bruscă a încărcărilor, fie prin sarcini a căror intensitate variază în timp.

Solicitări aplicate prin şocuri

În mod obişnuit, acestea se produc prin lovirea de către un alt corp solid a corpului ce trebuie calculat şi care în această prezentare va fi întotdeauna o bară, având oricare dintre formele întâlnite în capitolele anterioare. Există şi situaţii, aşa cum se va arăta mai jos, în care chiar bara de calculat este în mişcare, de exemplu în cădere de la o anumită înălţime şi se loveşte de un alt corp, aflat în repaos.
În toate aceste cazuri se ajunge la aplicarea prin şoc a unei solicitări dintre cele studiate anterior, care poate fi inclusiv una compusă. Se poate înţelege cu uşurinţă că efectele produse prin şoc vor fi mai importante decât cele rezultate din aplicarea statică a unei încărcări oarecare. Amploarea acestei diferenţe va rezulta din calcule specifice solicitărilor prin şoc.

Multiplicatorul de impact

Se consideră solicitarea produsă, asupra unei grinzi simplu rezemate, prin căderea unei greutăţi G, de la înălţimea H, ca în schema de mai jos.



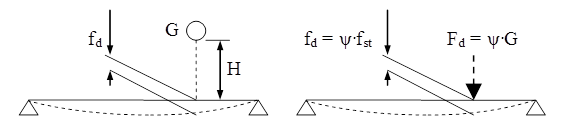Fig. 11.1

Se admite, pe baza observaţiilor anterioare, că deformaţia fd, produsă pe grindă de solicitarea prin şoc (dinamică) este de un număr ψ de ori mai mare decât deformaţia fst pe care o produce, în acelaşi punct de contact, forţa G aplicată fără şoc, adică cu masa respectivă aşezată simplu pe grindă. Este ca şi cum în punctul de contact ar fi aplicată o forţă dinamică Fd, mai mare şi ea de ψ ori decât greutatea G.
Numărul pozitiv ψ, care este mereu supraunitar (de obicei mult mai mare decât unitatea) se numeşte multiplicator de impact şi arată de câte ori sunt mai mari efectele (tensiuni şi deformaţii) produse de solicitarea dinamică, în comparaţie cu aceeaşi încărcare aplicată fără şoc şi numită solicitare statică echivalentă (SSE) a încărcării dinamice studiate.
Din cele de mai sus rezultă că valoarea factorului de impact va fi regăsită ca mărime a următoarelor rapoarte egale:
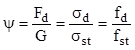                                (11.1)
Pentru a stabili modul cum trebuie calculat acest coeficient, se aplică stării dinamice de solicitare de mai sus (fig. 11.1) legea de conservare a energiei, care implică egalitatea dintre energia potenţială iniţială a corpului cu greutatea G (produsul dintre G şi înălţimea [H + fd] la care se aceasta se afla faţă de poziţia punctului de impact după aplicarea şocului) şi lucrul mecanic de deformare elastică, consumat pentru a produce deformaţia dinamică a grinzii. Acesta este egal, după cum s-a arătat la studiul energiei potenţiale de deformare elastică, cu semiprodusul dintre forţa dinamică Fd şi deformaţia fd pe care aceasta o produce pe grindă, deci legea de conservare se scrie:

Folosind exprimările (11.1) ale mărimilor dinamice în funcţie de cele statice care le sunt echivalente rezultă:

Prin analogie cu mărimile energetice explicate mai sus pentru solicitarea dinamică, în ultima expresie se pot recunoaşte mărimile care le corespund (şi care pentru simplitate vor fi notate fără indicele „st”) în starea statică (înainte de aplicarea şocului), adică energia potenţială Le = G×H, respectiv lucrul mecanic de deformare elastică Li = (G×fst)/2; făcând aceste substituţii şi trecând toţi termenii în membrul drept, se obţine:

Rezolvând această ecuaţie de gradul al doilea se obţin două valori ale factorului ψ, dintre care doar una este pozitivă şi se potriveşte condiţiilor din problemă, astfel că va reprezenta relaţia de calcul căutată:
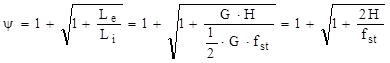         (11.2)
În aplicaţii se foloseşte una sau alta dintre formele acestei expresii, în funcţie de cazul particular de solicitare dinamică abordat.
Este interesant de subliniat că raţionamentul de mai sus se bazează pe ipoteza că energia cinetică a masei care cade este absorbită în totalitate de grinda care este lovită; aceasta reprezintă, de altfel, cazul cel mai puţin favorabil cu putinţă (situaţia în care efectele asupra grinzii sunt maxime), astfel că se impune a fi asumată pentru calculul dinamic al barei.

Observaţii asupra relaţiei (11.2)

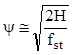                                      (11.3)

                                 (11.4)
Metoda de calcul bazată pe multiplicatorul de impact nu este singura prin care pot fi rezolvate problemele din această categorie, dar are avantajul că poate fi aplicată oricărei solicitări prin şoc, indiferent dacă este simplă sau compusă. Condiţia importantă pentru aplicarea metodei este ca deformaţiile care se produc pe corpul lovit în urma şocului să fie de tip liniar-elastic, întrucât toate raţionamentele de mai sus folosesc energia potenţială de deformare elastică acumulată în corpul solicitat prin şoc.
Recapitulând pe scurt cele prezentate până aici, se poate înţelege că, dacă se consideră o solicitare ca în figura 11.1 şi se notează cu B punctul de impact, atunci multiplicatorul va avea valoarea unică:
                               (11.5)
iar tensiunea dinamică şi deplasarea dinamică din oricare secţiune A de pe grinda analizată (inclusiv din secţiunea B) vor avea relaţiile:
             (11.6)
Prin urmare, solicitarea dinamică cea mai mare se va produce în secţiunea în care tensiunea este maximă în solcitarea statică echivalentă, iar condiţia calculului de rezistenţă va fi:
                            (11.7)
Este interesant de remarcat, chiar fără a detalia acest subiect, rolul pe care îl au elementele elastice de sprijin (deformabile sub acţiunea încărcărilor exterioare) în amortizarea şocurilor: de exemplu, dacă măcar unul dintre reazemele grinzii din fig. 11.1 este un resort elastic, atunci deformarea acestuia conduce la creşterea deformaţiei statice din punctul de impact, ceea ce scade valoarea fracţiei de sub radical din relaţia (11.5), adică duce la scăderea factorului de impact şi a efectelor produse prin şocuri.


Fig. 11.2

Aplicaţii

11.1. Să se scrie relaţia calculului de rezistenţă pentru bara prismatică din figură, de secţiune transversală oarecare şi constantă, pe capătul căreia ajunge masa m, căzând de la înălţimea H; se vor considera cunoscute valorile mărimilor necesare pentru acest calcul.

Rezolvare
Solicitarea statică echivalentă este axială (comprimare) cu forţa G = mg, iar deformaţia statică din punctul de impact are relaţia de calcul fst(B) = mgL/EA, deci factorul de impact va fi:

Tensiunea statică maximă este constantă în toate punctele barei şi deci condiţia calculului de rezistenţă în cazul barei considerate se va scrie astfel:

Pe această bază se vor putea rezolva toate tipurile de probleme întâlnite în calculul ingineresc – de verificare, dimensionare, sau încărcare maximă.



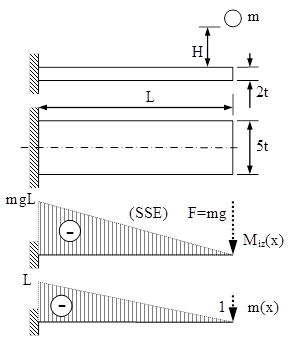Fig. 11.3

11.2. Se consideră o grindă în consolă (fig. 11.3), din lemn, având secţiunea dreptunghiulară, pe capătul căreia cade un corp cu masa m, de la înălţimea H; să se calculeze tensiunea maximă produsă în grindă în urma şocului, ştiind că: L = 1m, H = 0,4m, t = 40mm, E = 104MPa, m = 30kg.

Rezolvare
În partea de jos a figurii apar două grafice: diagrama de momente pentru SSE, respectiv cea a stării fictive de la aplicarea teoremei Mohr-Maxwell pentru calculul deplasărilor, cu forţă unitară în locul forţei exterioare F; pe baza lor, folosind algoritmul grafic de înmulţire a diagramelor (Vereşceaghin), deplasarea statică din punctul de impact (notat cu B, nemarcat pe desen) se calculează astfel:

Observând că momentul de inerţie al secţiunii faţă de axa de îndoire este

rezultă valoarea deplasării căutate:

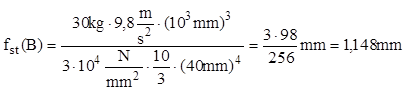
Această mărime se introduce în relaţia (11.5) a factorului de impact:

Tensiunea maximă din starea statică se produce în încastrare şi are mărimea:

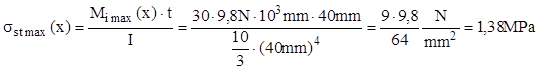
Tensiunea dinamică maximă din grinda analizată este:

Pe acelaşi principiu se poate stabili şi deformaţia dinamică maximă a barei:

Ambele rezultate permit să se afirme că efectele solicitării dinamice analizate păstrează materialul barei în domeniul în care deformaţiile sale sunt de tip liniar-elastic, deci calculele făcute prin metoda factorului de impact au fost corecte.


Fig. 11.4

11.3. Se consideră o bară cotită de forma literei L (fig. 11.4), de secţiune circulară cu diametrul d, încastrată la un capăt şi liberă la celălalt, unde se produce contactul cu masa m, care cade vertical, de la înălţimea H.
Să se calculeze valorile maxime ale tensiunii şi deplasărilor verticale de pe bară, dacă m=6kg, H=0,1m, a=0,3m, d=30mm, E=21×104MPa.

Rezolvare



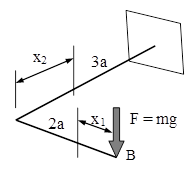Fig. 11.5

În această situaţie solicitarea statică echivalentă (fig. 11.5) este una compusă (de răsucire cu încovoiere) şi a fost tratată în detaliu în aplicaţia 5.1 dintr-un capitol anterior. Prin urmare, o parte dintre rezultatele parţiale necesare în calculele prezente vor fi preluate direct de acolo.
De exemplu, s-a stabilit că deplasarea statică (pe verticală) din punctul de impact are valoarea:

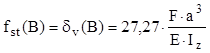
Datele numerice din situaţia de faţă conduc la următorul rezultat:

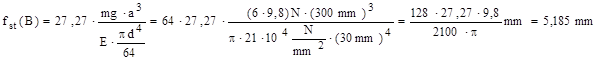
Pe de altă parte, folosind ipoteza de rupere τmax, s-a obţinut că tensiunea echivalentă maximă din bară (în secţiunea din încastrare) este:

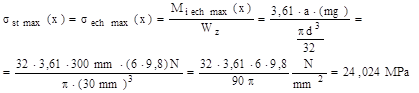
Multiplicatorul de impact se calculează astfel:

Prin urmare. Valorile maxime ale tensiunilor şi deplasărilor vor fi:


Se poate observa că nu există diferenţe de principiu, faţă de exemplele anterioare, în calculele la solicitările compuse aplicate prin şoc; practic oricare dintre aplicaţiile de la solicitările simple sau compuse ale barelor (cu orice formă de axă longitudinală) poate fi transformată în solicitare dinamică şi rezolvată prin metoda multiplicatorului de impact.
Pe de altă parte, cele trei aplicaţii de mai sus au în comun faptul că deformaţia statică a barelor, în punctul în care se produce impactul, poate fi calculată cu relativă uşurinţă. Există însă situaţii în care deplasarea din punctul de impact este dificil de stabilit, aşa cum este cazul aplicaţiei următoare. Prin urmare, va trebui ca multiplicatorul ψ să fie calculat cu prima formă de expresie din relaţia (11.2), adică aceea bazată pe mărimile energetice.

11.4. Să se scrie expresia multiplicatorului de impact pentru o bară dreaptă, ai cărei parametri constructivi se consideră cunoscuţi şi care cade de la o înălţime H asupra unui reazem plasat la mijlocul lungimii L a barei.



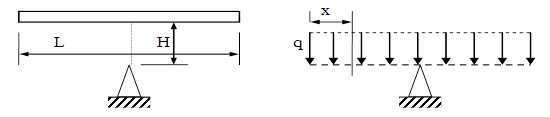Fig. 11.6

Rezolvare
În partea dreaptă a figurii este schiţată solicitarea statică echivalentă, în care bara se consideră încărcată numai cu greutatea ei, sub formă de forţă uniform distribuită, având intensitatea q, care poate fi calculată astfel:

Simbolul γ reprezintă greutatea specifică a materialului, iar cu A este notată aria secţiunii transversale a barei, admisă a fi de formă oarecare, dar constantă pe toată lungimea ei.
Se observă dificultatea de a defini şi calcula deplasarea statică a secţiunii în care se produce impactul, ceea ce conduce la folosirea mărimilor energetice pentru calculul factorului de impact ψ.
Lucrul mecanic exterior este dat de energia potenţială a barei, atunci când este ridicată la înălţimea H:

Lucrul mecanic elastic interior se calculează folosind formulele stabilite la solicitările simple şi care se bazează practic pe integrarea pe lungimea barei a pătratului expresiei eforturilor secţionale de pe fiecare regiune:

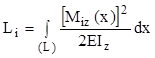
Această relaţie corespunde solicitării de încovoiere, care se produce în starea statică a barei considerate. Particularitatea încărcării ei este că există o simetrie perfectă între cele două jumătăţi de bară, separate de punctul de contact cu reazemul; studiul se poate face pe una dintre jumătăţi, pentru care secţionarea făcută în figura de mai sus arată că eforturile secţionale sunt:

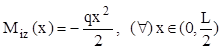
Se poate înţelege că momentul secţional este nul, la capetele barei şi atinge valoarea maximă chiar în punctul de impact, unde trebuie făcut calculul de rezistenţă pentru bara analizată. Problema de faţă nu include această cerinţă, fiind cerută doar expresia cu care se va calcula factorul de impact ψ. Pentru scrierea ei, trebuie detaliat calculul lucrului mecanic interior; observând că integrala pe lungimea barei se divide în două integrale identice, pe câte una dintre jumătăţile ei, se obţine următoarea expresie:

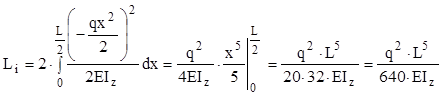
Prin urmare, prima relaţie (11.2) pentru calculul multiplicatorului de impact capătă pentru această bară forma:

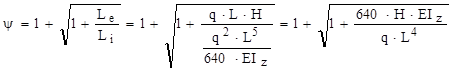
Se poate constata că în această expresie apar mărimi fizice ale căror valori au fost considerate cunoscute, prin enunţul problemei.

Solicitări variabile periodic

Există multe situaţii practice în care intensitatea solicitărilor mecanice nu doar că nu este constantă pe parcursul aplicării lor, dar variază continuu, cu frecvenţe mari şi în limite suficient de largi pentru a pune în pericol starea de funcţionare stabilă şi reversibilă a piesei respective.
Variaţiile pot fi oarecare (aleatoare), dar în mod frecvent parametrii lor se repetă după modele stabile şi durate fixe, adică se produc variaţii periodice ale solicitărilor. Un exemplu tipic de astfel de solicitare poate fi urmărit în cazul unui arbore de transmisie (fig. 11.7).
Pentru simplificarea discuţiei, se consideră un astfel de arbore pe care este montată o singură roată dinţată (având dantură dreaptă, ca să nu existe şi solicitări axiale în arbore), pe care acţionează componenta F a forţelor exterioare, orientată perpendicular pe axa de rotaţie.



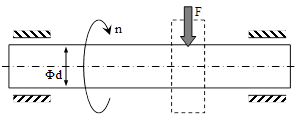Fig. 11.7

   Aspectul esenţial al acestui mod de încărcare este că direcţia forţei este mereu fixă, în vreme ce arborele se roteşte continuu (împreună cu roata) cu turaţia n (măsurată în ture pe minut). Din acest motiv, în fiecare punct de pe circumferinţa oricărei secţiuni transversale a arborelui valorile tensiunilor de încovoiere variază permanent, între mărimile lor extreme σmax şi σmin, egale şi de sensuri contrare, aşa cum se poate observa în figura următoare.



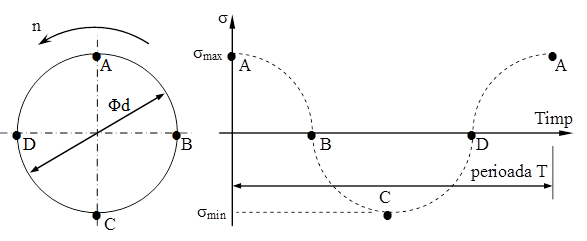Fig. 11.8

Graficul din dreapta reprezintă mărimile tensiunilor din toate punctele circumferinţei, atunci când secţiunea este poziţionată ca în imaginea din stânga. După ce se efectuează un sfert de rotaţie, punctul B ajunge în poziţia de la început a lui A, C în B etc. şi această schimbare de locuri se petrece în mod continuu, astfel încât după o rotaţie completă fiecare punct de pe circumferinţă parcurge toate poziţiile indicate cu linii punctate pe grafic şi revine la locul său iniţial, după care ciclul se reia în întregime.
Prin urmare, fiecare rotaţie a arborelui determină apariţia în punctele de pe suprafaţa sa exterioară a unei solicitări variabile a cărei perioadă T are chiar mărimea unei rotaţii complete a piesei; există şi alţi parametri prin care sunt caracterizate ciclurile de solicitare şi care se definesc astfel:

Parametrul R este cel mai important pentru identificarea unei solicitări variabile, fiind numit şi caracteristica ciclului de solicitare, iar două cicluri de variaţie distincte, care au aceeaşi valoare a coeficientului de asimetrie sunt denumite cicluri asemenea. Pe de altă parte se observă că tensiunile extreme ale ciclului se pot exprima în funcţie de primii doi parametri definiţi mai sus, sub forma:   σmax = σm + σv ,   respectiv   σmin = σm - σv .
Ciclurile de forma reprezentată în figura 11.8 sunt caracterizate prin tensiuni extreme de valori egale şi de semne opuse, adică au R = -1 şi sunt denumite alternant-simetrice; ele materializează cele mai periculoase dintre solicitările variabile, întrucât provoacă într-un timp mai scurt, în comparaţie cu alte forme de cicluri, cedarea materialului astfel solicitat.
La celălalt capăt al scalei, „ciclurile” cu R = 1 sunt cele mai uşor de suportat, întrucât sunt de fapt solicitări statice; între aceste forme extreme se plasează trei tipuri intermediare de cicluri ale solicitărilor variabile, ilustrate în figura 11.9 şi explicate mai jos:



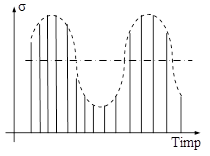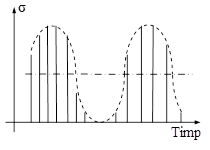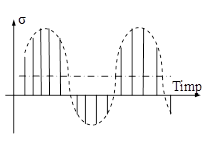a.                                        b.                                     c.
Fig. 11.9
  1. oscilante – cu tensiuni limită de acelaşi semn (deci pot fi ambele negative), la care parametrul R este cuprins între 0 şi 1 (fără să atingă şi aceste valori);
  2. pulsante – caz particular al celor de mai sus, având tensiunile minime nule, ceea ce înseamnă R = 0;
  3. alternante – cu tensiuni limită de semne opuse, dar diferite ca mărimi, deci având valorile R cuprinse între (-1) şi 0.

Observând cu atenţie aceste precizări, se poate admite că toate ciclurile de solicitare reprezentative pentru practică sunt ilustrate de variaţiile care au coeficientul R cuprins în intervalul [-1; 1], iar determinările experimentale pe astfel de cicluri sunt focalizate.

Determinarea rezistenţelor la oboseală

Se poate intui că, în încercările de laborator, fiecare lot de probe dintr-un material (de obicei metalic) care se propune a fi studiat este solicitat prin cicluri având valori modificabile ale tensiunilor, dar o mărime fixată a factorului R, reprezentând deci cicluri asemenea. Condiţiile standard se referă la epruvete cilindrice, având în mod uzual diametrul d = 10mm.
Cerinţe importante şi riguroase se impun în legătură cu calitatea de suprafaţă a epruvetelor: acestea trebuie să fie netede (deci lipsite de concentratori de tensiuni) şi prelucrate fin. Fiecare probă este încercată până la rupere, la parametri constanţi (dar descrescători de la o epruvetă la următoarea) ai solicitării variabile, urmărindu-se numărul maxim N de cicluri pe care proba le suportă.
Oricare dintre parametrii tensiunilor poate fi folosit ca termen de comparaţie între diversele cicluri de solicitare, dar în mod obişnuit este aleasă în acest scop valoarea lor maximă σmax. Prima testare se face la o tensiune maximă relativ mare (notată cu σ1), de ordinul a două treimi din rezistenţa statică la întindere a materialului încercat. Numărul N1 de cicluri suportate până la rupere este în acest caz relativ mic.



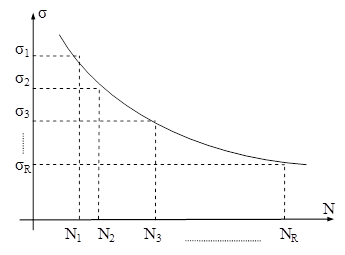Fig. 11.10

   Se fac apoi încercări la care tensiunea maximă scade treptat (cum se arată în fig. 11.10) şi se constată că numărul N creşte mereu; când se ajunge cu σmax la un nivel σR, a cărui valoare depinde de categoria din care face parte materialul, se face constatarea că epruvetele nu se mai rup chiar după un număr foarte mare de cicluri.
Mărimea σR astfel stabilită, definită ca valoarea tensiunii maxime la care materialul testat suportă un număr „nesfârşit” de cicluri de încărcare este considerată a fi rezistenţa lui la oboseală, pentru cicluri de solicitări variabile având caracteristica de asimetrie egală cu R.
Desigur că numărul infinit de cicluri este în realitate substituit prin valori (de ordinul milioanelor) considerate acceptabile pentru diversele clase de materiale: astfel, pentru fonte se admit, de regulă, 5×106 cicluri, pentru oţeluri 10×106, iar pentru metalele şi aliajele neferoase între 50 şi 100×106 cicluri de solicitare.
Graficul de durabilitate de mai sus, pe baza căruia se defineşte rezistenţa la oboseală a materialelor este numit de obicei curba lui Wöhler, după numele inginerului german care a realizat, la mijlocul secolului 19, primele încercări sistematice privind rezistenţa la solicitările variabile.
În legătură cu acest grafic sunt de semnalat câteva particularităţi foarte importante şi care ajută la înţelegerea corectă a modului cum sunt interpretate rezultatele experimentale ale acestor încercări.
Mai întâi se poate observa că trasarea curbei se face prin medierea (interpolarea) punctelor de pe grafic ce corespund datelor din laborator, care numai prin excepţie ar putea fi toate aşezate exact pe această curbă. Uzual se întâmplă, dimpotrivă, să se obţină împrăştieri mari ale acestor puncte şi implicit o relativă nesiguranţă în stabilirea caracteristicilor de rezistenţă la oboseală care sunt necesare în proiectarea inginerească.
Explicaţia acestei situaţii stă în legătura strânsă dintre rezultatele încercărilor şi o serie de parametri foarte greu de repetat identic, ţinând de experimente (precizia realizării epruvetelor, menţinerea sub control a parametrilor solicitării) şi de materialele încercate (omogenitate, efecte ale proceselor metalurgice de fabricare).
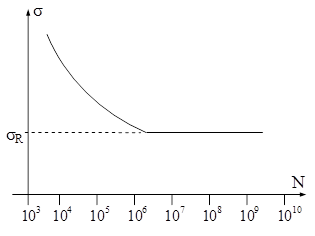
Pe de altă parte se constată că, în funcţie de aspectul curbei Wöhler se deosebesc două mari clase de materiale. Una dintre ele (fig. 11.11 a) se bazează pe aliajele feroase şi cele de titan, pentru care curba devine practic orizontală, când N are valori mari, ceea ce corespunde definirii teoretice a rezistenţei la oboseală σR. Pentru oţeluri această valoare este în mod obişnuit cuprinsă între 35% şi 60% din rezistenţa lor la tracţiune statică.



a.                                                        b.
Fig. 11.11

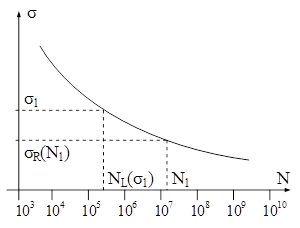
Cealaltă categorie include cele mai multe aliaje neferoase (în mod tipic cele de aluminiu, cupru, magneziu), la care nu se poate defini o rezistenţă la oboseală propriu-zisă, întrucât curba nu ajunge la o porţiune orizontală şi este permanent descendentă (fig. 11.11 b). Din acest motiv, comportarea materialului este caracterizată prin limita de oboseală σR(N1) – nivelul de tensiune la care materialul cedează pentru un număr dat N1 de cicluri (situat aproximativ la valoarea de 10 milioane).
Un alt parametru caracteristic pentru aceste materiale este durata de viaţă la tensiunea σ1, NL(σ1) – numărul de cicluri suportate până la rupere atunci când tensiunea maximă a ciclului de solicitare are nivelul precizat.

Diagrame ale rezistenţelor la oboseală

Din cele de mai sus rezultă că pentru fiecare material se poate vorbi despre o infinitate de valori ale rezistenţelor la oboseală, câte una pentru fiecare nivel al coeficientului de asimetrie R. Este practic imposibil ca toate aceste valori să fie stabilite pe cale experimentală, astfel încât sunt necesare metode prin care să poată fi dedusă rezistenţa care corespunde unui factor arbitrar R, pe baza unui trend general de evoluţie valabil pentru materialul considerat.
Există mai multe variante de soluţii pentru această problemă, dintre care în mod frecvent se apelează la aceea bazată pe curba ciclurilor limită (a lui Haigh), trasată pentru materialul piesei studiate: se admite că fiecare valoare a rezistenţei la oboseală reprezintă un punct în planul de coordonate σm–σv (tensiunea medie şi amplitudinea ciclurilor de solicitare), iar aceste puncte se plasează pe o curbă continuă având aspectul din figura următoare.



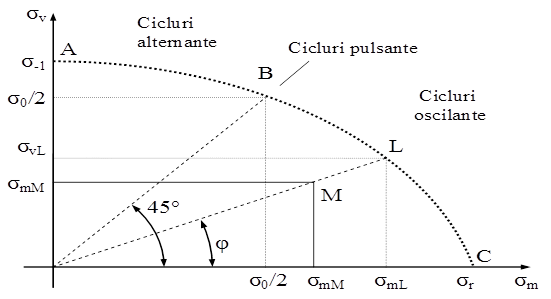Fig. 11.12

Forma acestei curbe sugerează că rezistenţa cea mai mare se înregistrează în cazul ciclului de solicitare de amplitudine zero (σv=0), la care tensiunile extreme coincid între ele şi sunt egale cu tensiunea medie σm; acestea sunt caracteristicile solicitării statice, la care limita de rupere se notează cu σr, aşa cum este marcat şi pe grafic.
Fiecare dintre celelalte puncte de pe curbă reprezintă rezistenţa la oboseală a ciclurilor de solicitare având o anumită caracteristică R, ceea ce poate fi observat dacă se scrie tangenta unghiului φ sub forma:
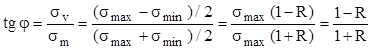                    (11.8)
Rezultă că orice segment ce uneşte originea axelor cu un punct de pe curbă conţine punctele reprezentative ale ciclurilor asemenea de caracteristică R.
Este remarcabil faptul că suma coordonatelor fiecărui punct de pe curbă (ca şi ale fiecărui punct din planul de coordonate considerat) este egală cu tensiunea maximă σmax a ciclului de solicitare respectiv. Prin urmare, dacă se ia în considerare segmentul cu unghiul de înclinare φ, valoarea σR a rezistenţei la oboseală a ciclurilor astfel reprezentate este marcată pe grafic prin punctul limită L şi este egală cu:   σR = σmL + σmL .  Ciclul oarecare M, având acelaşi factor de asimetrie cu ciclul limită L, este considerat cu atât mai sigur, pentru materialul studiat, cu cât este mai distanţat faţă de L.
Pe baza relaţiei (11.8) de mai sus pot fi identificate poziţiile pe care le ocupă segmentele reprezentative ale unor tipuri importante de solicitări variabile:

 

Aşa cum se arată şi în figura 11.12, segmentele cu înclinări aflate între aceste limite corespund ciclurilor oscilante, respectiv celor alternante. Pe de altă parte este de menţionat că, pentru materialele care la solicitarea statică au palier de curgere pe curba caracteristică, limita de rezistenţă de pe axa absciselor se asimilează cu limita de curgere σc a materialului analizat.



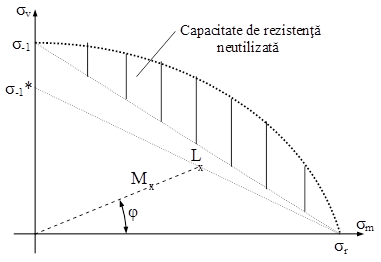Fig. 11.13

   Din cele explicate mai sus se poate înţelege că trasarea curbei Haigh este foarte importantă pentru calculul la oboseală. Pe de altă parte, consumul mare de timp şi de material face dificilă obţinerea pe cale experimentală a unui număr suficient de puncte ale acestei curbe.
Prin urmare, se face apel la variante schematizate ale diagramei ideale a ciclurilor limită; una dintre acestea, propusă de Soderberg, este schiţată în figura alăturată. Pentru trasarea ei se folosesc doar două valori ale limitei de rupere obţinute prin încercări ale materialului, una pentru solicitarea statică, alta pentru cicluri variabile alternant-simetrice.
Desigur că graficul astfel trasat este uşor de obţinut, dar el are un dezavantaj major, acela că lasă în afara domeniului ciclurilor admise, pentru materialul analizat, un număr mare de cicluri de solicitare care din punct de vedere teoretic sunt suportabile în condiţii bune de către material; în schimb, simplificarea majoră a etapelor necesare pentru trasarea curbei limită este de obicei suficient de importantă pentru ca dezavantajul respectiv să fie asumat şi schematizarea să fie larg utilizată în practică.
Un alt aspect important pentru calcule este acela că limita de rupere σ-1 de la ciclurile alternant-simetrice are valori mult diferite, pentru piesele reale (cărora le corespunde notaţia σ-1*), faţă de cele obţinute pe epruvete, în condiţiile precizate de standarde. Diferenţele respective sunt luate în considerare prin factori de influenţă cu care se amendează valorile teoretice, aşa cum se va prezenta în continuare.

Rezistenţa la oboseală calculată pentru piesele reale

S-a arătat anterior că există o gamă largă de factori care influenţează modul în care se comportă materialele la solicitări variabile; printre cei mai importanţi sunt forma şi frecvenţa ciclurilor de încărcare, dar şi structura şi granulaţia materialului, care sunt strâns legate de eventualele tratamente termice aplicate anterior acestuia.
Pe de altă parte, comportarea pieselor reale diferă mult de aceea a epruvetelor încercate în laborator, ceea ce se consideră a se explica prin trei categorii mari de deosebiri între piese şi probe: dimensiunile mai mari, gradul de netezire a suprafeţelor şi prezenţa concentrărilor de tensiuni.

a) Factorul dimensional

Se admite că volumul mai mare de material al piesele reale în comparaţie cu epruvetele standardizate (de obicei cilindrice cu d=10mm) face să crească probabilitatea apariţiei defectelor de structură şi microfisurilor, ducând la limite de rupere mai mici decât cele teoretice. Acest fapt este luat în considerare în calcule printr-un factor notat de obicei cu ε, totdeauna mai mic decât unitatea, care se înmulţeşte cu rezistenţa teoretică σR.
Valoarea acestui factor scade mereu, atunci când dimensiunea piesei care se calculează creşte; scăderea este cu atât mai puternică cu cât forma piesei include concentratori de tensiuni. Aceste evoluţii sunt ilustrate în prima diagramă din fig. 11.14, în care cele patru curbe trasate corespund următoarelor categorii de materiale metalice: 1 – oţeluri carbon, în piese fără concentratori de tensiuni; 2 – oţeluri carbon, cu concentratori moderaţi şi oţeluri aliate fără concentratori; 3, respectiv 4 – oţeluri aliate, în piese cu concentratori moderaţi, respectiv puternici.
Trebuie precizat că toate diagramele despre factorii de influenţă discutaţi aici sunt strict orientative şi nu pot fi folosite pentru alegerea valorilor acestor coeficienţi în calcule de proiectare. În acest scop se utilizează datele cuprinse în baze de date sau în cărţi specializate, de felul îndrumarelor de proiectare; în legătură cu acestea se recomandă să se apeleze la surse cât mai cuprinzătoare, astfel încât tema să fie rezolvată, pe cât se poate, pe baza informaţiilor luate dintr-un singur izvor, care probabil se vor corela în mod corect şi vor duce la rezultate de încredere.


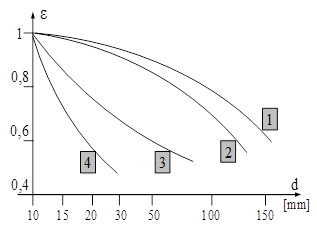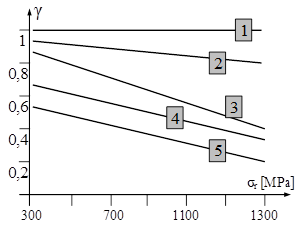
Fig. 11.14

b) Factorul de calitate a suprafeţelor

Cunoscând faptul că pentru încercările de laborator se folosesc epruvete fin prelucrate, se înţelege că piesele cu suprafeţele prelucrate mai grosier vor fi predispuse să cedeze la încărcări variabile mai mici decât cele rezultate din calcule teoretice.
Pe de altă parte, multe dintre stările de solicitare uzuale fac să se producă tensiunile cele mai mari în punctele de pe suprafaţa exterioară a pieselor, ceea ce favorizează apariţia în acele puncte a unor microfisuri în care apoi să se amorseze ruperea prin oboseală a corpului respectiv.
Prin urmare, capacitatea de rezistenţă a unei piese ce trebuie să preia solicitări variabile este în mod hotărâtor influenţată de tipul şi de fineţea prelucrărilor aplicate pe suprafeţele ei. În plus, rezistenţa la oboseală scade puternic (în special la aliajele feroase) atunci când piesa trebuie să lucreze în medii care produc coroziune.
Aceste influenţe sunt de obicei exprimate în calcule printr-un alt factor subunitar, care se notează cu γ şi se înmulţeşte cu rezistenţa teoretică la oboseală. Câteva exemple tipice de valori ale acestui coeficient, inclusiv variaţia lui în funcţie de rezistenţa la rupere prin tracţiune a materialului piesei sunt date, pentru oţeluri, în cea de-a doua diagramă din fig. 11.14.
Se observă că factorului γ i se atribuie o variaţie liniară, iar graficele din figură corespund următoarelor cazuri particulare de piese: 1 –cu suprafeţe lustruite; 2 şi 3 –cu suprafeţe prelucrate prin strunjire - fină, respectiv de degroşare; 4 şi 5 –supuse coroziunii în apă dulce, respectiv sărată.

c) Factorul de concentrare a tensiunilor

Prezenţa în configuraţia unei piese a concentratorilor de tensiuni (degajări, racordări cu raze mici, găuri transversale, canale de pană, filete, îmbinări cu strângere etc.) contribuie de asemenea la scăderea rezistenţei sale la solicitările variabile. Practic orice crestătură sau discontinuitate geometrică de pe suprafaţa piesei poate acţiona ca amorsă pentru o fisură de oboseală.
Aceste efecte sunt luate în considerare în calcule printr-un factor de influenţă, notat cu Kσ şi având mereu valori mai mari decât unitatea, deoarece rezistenţa teoretică la oboseală se împarte la acest coeficient pentru a găsi rezistenţa care corespunde piesei analizate!
O altă particularitate a acestui factor este că depinde hotărâtor de felul concentratorului prezent pe piesă (deci calculul trebuie făcut separat pentru fiecare secţiune în care există astfel de elemente de sensibilizare); prin urmare valorile lui Kσ se găsesc în diagrame foarte numeroase şi variate (grupate pe tipuri de concentratori), care solicită din plin atenţia şi răbdarea proiectantului pentru alegerea valorii potrivite cu situaţia analizată.



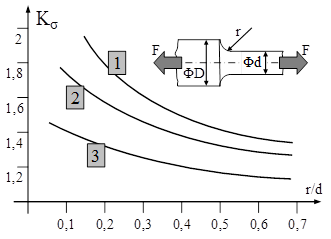Fig. 11.15

   Figura alăturată prezintă cazul unor piese de oţel care preiau o solicitare axială variabilă şi la care concentrarea tensiunilor este determinată de razele mici de racordare, în secţiunea de trecere dintre două tronsoane de diametre diferite.
Graficele arată că factorul de influenţă este cu atât mai mare cu cât raza r este mai mică faţă de diametrul tronsonului îngust.
Cele trei curbe corespund, în ordine descrescătoare, oţelurilor cu rezistenţa la tracţiune statică de 1200 (curba 1), 800 şi respectiv 400MPa, ceea ce arată că influenţa concentrărilor de tensiuni este cu atât mai periculoasă pentru funcţionarea piesei calculate cu cât materialul este mai rezistent şi mai dur.
La finalul acestui paragraf se face menţiunea că întreaga prezentare asupra calculului la oboseală poate fi făcută, în mod similar, pentru solicitările date prin tensiuni tangenţiale, înlocuind peste tot pe σ cu τ!
În altă ordine de idei, utilizând factorii de influenţă discutaţi mai sus se face trecerea de la valoarea de laborator σR a rezistenţei la oboseală a unui material, la valoarea σR* a acestei rezistenţe, corespuzând unei piese făcute din acel material, ale cărei forme, dimensiuni, prelucrări de suprafaţă şi condiţii de lucru conduc la alegerea valorilor potrivite ale coeficienţilor din următoarea relaţie de calcul:
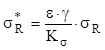                                      (11.9)

Coeficientul de siguranţă la oboseală

La fel ca în cazul altor categorii de calcule inginereşti, la care ipotezele şi relaţiile folosite aproximează realitatea fizică, menţinând un grad ridicat de incertitudine asupra preciziei acestor aproximări, calculul la oboseală trebuie să asume imprecizia rezultatelor la care el conduce şi să admită impunerea unei distanţe de siguranţă între caracteristicile pieselor obţinute prin calcule şi cele care corespund situaţiilor limită, admise drept fatale pentru integritatea în funcţionare a pieselor respective.
Mai precis, dacă pentru o piesă reală este calculat drept admisibil un anumit ciclu de solicitare variabilă (având pe o schematizare ca în fig. 11.13 punctul reprezentativ M), este necesar să se verifice cât de distanţat este acest ciclu de acela cu parametri similari (L), despre care se consideră că produce ruperea prin oboseală, în limitele stabilite pentru materialul piesei respective. În mod uzual se foloseşte ca parametru de similitudine factorul de asimetrie R, iar ca termen definitoriu al unui ciclu de solicitare tensiunea extremă σmax, deci comparaţia se face pe segmentul cu înclinarea φ.



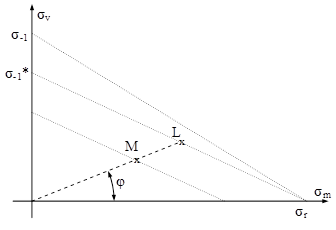Fig. 11.16

   Reluând schematizarea de mai sus (fig. 11.16), cu includerea liniei „rectificate” care se referă la piesele reale, se observă că linia paralelă cu aceasta dusă prin punctul M reprezintă toate ciclurile asemenea celor limită şi care au aceeaşi siguranţă ca şi ciclul din M.
Definiţia coeficientului de siguranţă pentru ciclul M va fi:

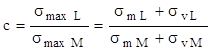
Folosind asemănarea triunghiurilor dreptunghice având ipotenuzele pe segmentul punctat şi după câteva transformări elementare se ajunge la:
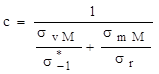                                       (11.10)
Rezistenţa la oboseală a piesei la ciclul alternant simetric se calculează cu o relaţie de forma (11.9), astfel încât expresia finală a coeficientului de siguranţă la oboseală pentru ciclul oarecare M se scrie astfel:
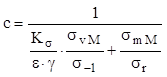                                     (11.11)
Dacă materialul piesei calculate este de tip tenace, atunci limita lui de rezistenţă la solicitarea statică este cea de curgere σc, iar schematizările şi deducţiile de mai sus se adaptează acestei situaţii, încât singura modificare în relaţia (11.11) va fi σc în loc de σr, în ultima fracţie de la numitor.
Trebuie precizat că acest calcul se face întotdeauna sub formă de verificare, în sensul că piesa este dimensionată pe baza solicitărilor ei statice, iar calculul la oboseală se face în câteva secţiuni ale piesei, de obicei alese dintre acelea care conţin concentratori de tensiuni.
În principiu, valorile recomandate pentru coeficientul de siguranţă sunt cuprinse între 1 şi 3 – mai mici decât 2 pentru piesele din oţeluri şi peste 2 pentru piese din fontă sau aliaje neferoase. Valorile impuse se dau de obicei ca numere zecimale, cu o singură cifră după virgulă şi sunt cu atât mai mari cu cât este mai mare gradul de nesiguranţă asupra calităţilor materialului şi a elementelor solicitării.

Dacă solicitarea variabilă pe care piesa o suportă este de tip compus, de exemplu de răsucire cu încovoiere, care apare în mod obişnuit la arborii din cutiile de viteze, atunci se analizează pe rând elementele caracteristice ale celor două solicitări şi pentru fiecare în parte se stabileşte, în secţiunea de calcul aleasă, valoarea unui coeficient de siguranţă la oboseală, după modelul descris mai sus. Valoarea coeficientului global de siguranţă din acea secţiune se determină folosind expresia:
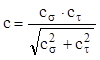                                       (11.12)

Exemplu de calcul

Se imaginează un arbore de transmisie dintr-o cutie de viteze, având în secţiunea solicitată cel mai puternic un concentrator de tensiuni de forma unui canal de pană. Arborele este din oţel carbon obişnuit OL60, care are următoarele valori (exprimate în MPa) ale caracteristicilor de rezistenţă:
σr = 600;   σc = 320;   σ-1 = 280;   τc = 200;   τ-1 = 160
Secţiunea de calcul are diametrul de 40mm, iar canalul de pană, prelucrat cu o freză deget, are lăţimea de 12mm şi adâncimea de 4mm. Se cunoaşte că în secţiunea respectivă momentul de încovoiere are valoarea Mi(x)=400Nm, iar cel de răsucire este Mt(x) = 280Nm.
Se cere să se calculeze valoarea coeficientului global de siguranţă la oboseală pentru secţiunea periculoasă a arborelui.

Rezolvare

a) Coeficientul de siguranţă la solicitarea variabilă de încovoiere
Pentru completarea mărimilor din relaţia (11.11), se face observaţia că prin încovoiere se produc cicluri alternant-simetrice (care au tensiunea medie nulă), pentru care amplitudinea este egală cu tensiunea maximă produsă de momentul de încovoiere din secţiune.
Pentru simplificarea acestui calcul, se adoptă pentru modulul de rezistenţă o variantă de calcul acoperitor, în care se admite că diametrul net al secţiunii se măsoară la baza canalului de pană: dnet=(40-2×4)mm=32mm şi în aceste condiţii amplitudinea ciclurilor de solicitare va fi:

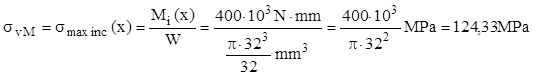
Rămân de stabilit valorile factorilor de influenţă, pentru care se poate folosi, de exemplu, întrucât cuprinde o gamă largă de date, cartea „Rezistenţa materialelor. Partea a doua”, autor Al. Anghel, Ed. Univ. din Ploieşti, 2005. Astfel, pentru factorul dimensional, se urmăreşte diagrama din fig. 16.18, pg. 326; pe curba 2 (oţel carbon cu concentratori moderaţi) pentru diametrul d=40mm se găseşte valoarea ε=0,84.
Pe diagrama din fig. 16.19, pg. 328, curba pentru prelucrarea prin strunjire fină, pentru σr=600MPa se citeşte valoarea γ=0,8. Pentru factorul de concentrare a tensiunilor, în fig. 16.17, pg. 326 se află o diagramă referitoare la canalele de pană prelucrate cu freză deget, pe care se citeşte, pentru σr=600MPa, valoarea Kσ=1,6.
Înlocuind toate valorile discutate mai sus în relaţia (11.11), în care trebuie folosită limita de curgere, materialul fiind de tip tenace, se obţine coeficientul de siguranţă pentru ciclul alternant-simetric de încovoiere:

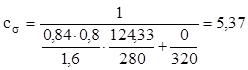
b) Coeficientul de siguranţă la solicitarea variabilă de răsucire
De obicei această solicitare se consideră a fi de tip pulsant, întrucât se ţine seama de cuplările şi decuplările repetate ale transmisiei. Prin urmare, tensiunea medie şi amplitudinea ciclului sunt egale între ele şi egale cu jumătate din tensiunea maximă de răsucire din secţiune, iar datele de mai sus conduc la următorul calcul:

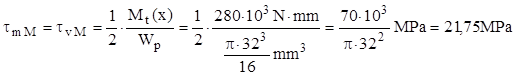
Factorul dimensional se ia cu aceeaşi valoare ca pentru încovoiere, ε=0,84; pentru influenţa calităţii de suprafaţă sursa citată indică următoarea legătură între coeficienţii de la cele două tipuri de solicitări variabile (pg. 328):

În fine, coeficientul de concentrare a tensiunilor pentru arbori cu canale de pană solicitaţi la răsucire este dat în tabelul de la pg. 356: pentru σr=600MPa se obţine valoarea Kτ=1,5.
Cu toate datele astfel găsite se calculează coeficientul de siguranţă pentru solicitarea pulsantă de răsucire:

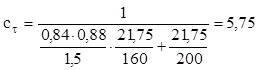
c) Coeficientul de siguranţă la solicitarea variabilă compusă de răsucire cu
încovoiere
Se aplică relaţia (11.12), din care se obţine valoarea globală:

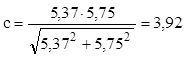
Acest rezultat respectă recomandările din literatura domeniului, prin urmare solicitarea variabilă din secţiunea periculoasă a arborelui este cuprinsă în domeniul de siguranţă faţă de limita de rezistenţă la oboseală.

Precizări privind ruperea pieselor prin oboseală

Oboseala materialelor reprezintă un fenomen imposibil de neglijat pentru practica inginerească, pentru că se estimează a fi cauza ruperii pentru aproximativ 90% dintre componentele metalice care cedează în timpul exploatării. Pericolul este cu atât mai mare cu cât apariţia şi dezvoltarea fisurilor de oboseală se observă cu dificultate, în lipsa unor investigaţii speciale, astfel încât de cele mai multe ori procesul de cedare avansează fără vreun avertisment şi devine catastrofal.
Ruperile au caracter fragil chiar pentru metale care în general se încadrează între cele ductile, cedarea fiind precedată în foarte mică măsură de deformaţii plastice ale materialului. Secţiunile rupte au un aspect specific, destul de uşor de recunoscut, întrucât conţin de obicei două zone puternic individualizate – una netedă, lucioasă, rezultată prin frecarea între ele, pe parcursul funcţionării, a celor două feţe ale secţiunii fisurate şi o altă zonă grăunţoasă, care ocupă restul secţiunii de rupere şi corespunde părţii de material care cedează brusc, la finalul procesului.
Poziţionarea şi proporţia relativă a celor două zone depind în principiu de felul solicitării variabile care se aplică piesei respective, dar şi de mărimea tensiunilor maxime ale ciclurilor de solicitare. Din acest punct de vedere se diferenţiază două categorii mari de solicitări variabile.


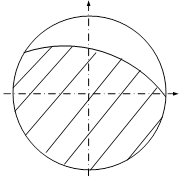
Fig. 11.17

            O primă categorie e formată de solicitări cu încărcări relativ mari, care la fiecare ciclu produc în material inclusiv deformaţii plastice, într-o proporţie anumită; din acest motiv durata de viaţă a pieselor este mică (în principiu cel mult 104÷105 cicluri), iar fenomenul pe care îl suportă este numit oboseală oligo-ciclică. Secţiunile rupte au în mod specific o parte relativ mică de aspect lucios (fig. 11.17), întrucât frecarea celor două feţe ale fisurii are loc pentru un timp destul de scurt.


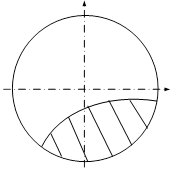
Fig. 11.18

   Cea de-a doua grupă include solicitările care produc tensiuni de valori medii şi mici, făcând să apară în material numai deformaţii de tip elastic; durata de viaţă a pieselor astfel solicitate este mare (cel puţin 104÷105 cicluri), adică oboseala este înalt-ciclică. Fisurile se dezvoltă pe perioade mari de timp, făcând ca specificul secţiunilor de rupere (fig. 11.8) să fie aria relativ mică pe care o ocupă zona cristalină.

Posibilităţi de creştere a rezistenţei pieselor la oboseală

Durata de viaţă a componentelor care preiau solicitări variabile poate fi crescută, dacă se analizează cu atenţie cauzele cunoscute ale apariţiei şi dezvoltării fisurilor de oboseală în structura materialelor. Metodele prin care se acţionează în această direcţie sunt în principiu de două tipuri.

A. Metode aplicate la proiectare
Atunci când se proiectează un anumit ansamblu de repere, pe baza sarcinilor pe care acesta trebuie să le preia, cea mai importantă problemă în privinţa rezistenţei pieselor la oboseală este evitarea în cât mai mare măsură a acelor neregularităţi de suprafaţă şi de structură (filete, canale de pană, îmbinări cu strângere, muchii ascuţite, găuri transversale, salturi brutale de secţiune) care tind să producă amplificări (concentrări) locale de tensiuni.
Pe de altă parte, cunoscând că funcţionarea la temperaturi ridicate sau în medii corozive contribuie din plin la scăderea rezistenţei la oboseală a materialelor metalice, trebuie folosită orice posibilitate de se evita sau limita, pentru componentele supuse la solicitări variabile, expunerea la astfel de condiţii de lucru.

B. Metode tehnologice
Este de mult timp constatat faptul că piesele cu suprafeţe perfect finisate au rezistenţa la oboseală mai bună decât cele care au fost prelucrate grosier, astfel încât îmbunătăţirea calităţii suprafeţelor este o măsură care va avea întotdeauna efecte benefice asupra duratei de viaţă a pieselor ce preiau solicitări variabile
La aceasta se adaugă un alt procedeu dovedit a fi foarte eficient, în acelaşi scop – inducerea, într-un strat subţire de la suprafaţa pieselor respective, a unor tensiuni remanente de compresiune. Acestea vor micşora, într-o anumită măsură, efectele produse în straturile superficiale de tensiunile de întindere date de solicitarea variabilă, făcând să scadă tendinţele de apariţie şi dezvoltare a fisurilor de oboseală.

a) Aplicarea unor tratamente mecanice superficiale
Un mijloc frecvent utilizat pentru tensionarea superficială prin comprimare a pieselor (mai ales dacă sunt din metale de tip tenace) constă în a produce deformări plastice localizate, în straturile lor de suprafaţă. Metoda uzuală este bombardarea suprafeţelor cu jet de alice: particule dure, de dimensiuni mici (cu diametre între 0,1 şi 1mm) sunt proiectate cu viteze foarte mari asupra pieselor tratate.
Prin deformaţiile produse se imprimă, în straturile respective de material (pe adâncimi cuprinse între un sfert şi o jumătate din diametrul particulelor dure folosite), tensiuni remanente de comprimare, prin care se va ajunge la creşterea rezistenţei la oboseală a componentelor respective.

b) Aplicarea unor tratamente termo-chimice

Piesele sunt plasate în incinte cu atmosferă bogată în carbon sau azot, la temperaturi ridicate care să favorizeze difuzia acestor elemente chimice, cam pe 1mm adâncime, în straturile superficiale de material. Procesele se numesc carburare, respectiv nitrurare şi conduc la creşterea rezistenţei la oboseală prin durificarea suprafeţei pieselor, dar şi prin inducerea în acele straturi a unor tensiuni reziduale de compresiune.