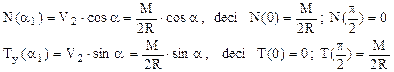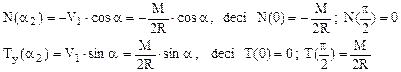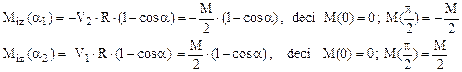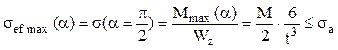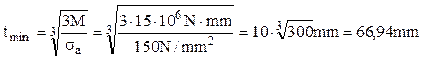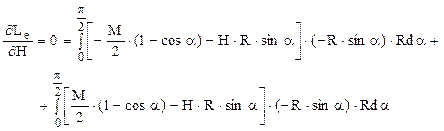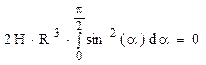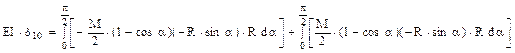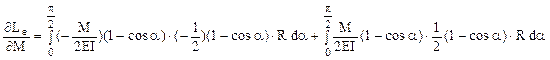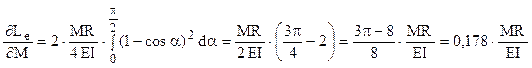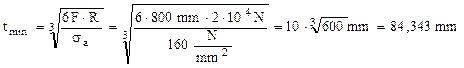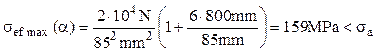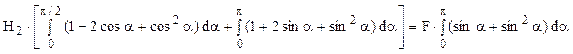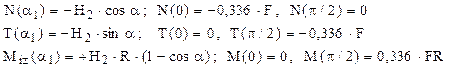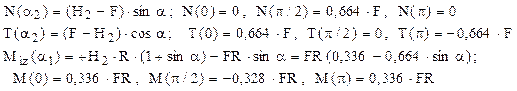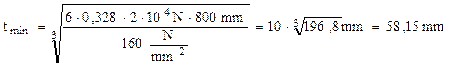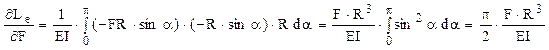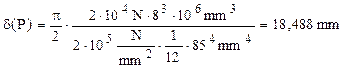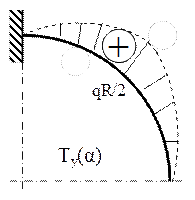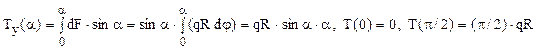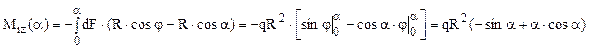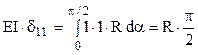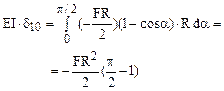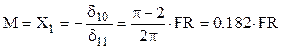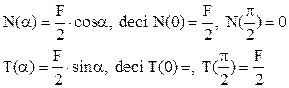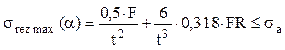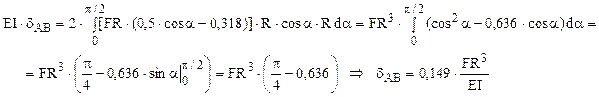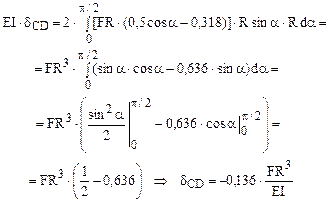Particularităţi de calcul
Pentru analiza barelor cu axă curbă sunt considerate valabile toate regulile discutate la calculul barelor cotite, cu precizarea importantă că, pentru barele curbe, direcţia tangentei la axa longitudinală se modifică mereu, de la fiecare secţiune transversală la cea vecină.
Din acest motiv, de la o secţiune la alta se schimbă şi valoarea proiecţiilor date de încărcările exterioare, care compun expresiile eforturilor secţionale. Schimbarea se materializează în apariţia, în respectivele expresii, a funcţiilor trigonometrice (sinus şi cosinus) de α, unghiul care defineşte poziţia secţiunii transversale în care se face calculul.
Trebuie precizat că, dacă axa longitudinală a unei bare are formă circulară, atunci poziţia pe axă a punctelor de calcul se exprimă mai eficient folosind coordonatele polare, în comparaţie cu cele carteziene; cercurile având raza R constantă, rezultă că la aceste bare variabila α este suficientă pentru marcarea secţiunilor şi definirea eforturilor secţionale.
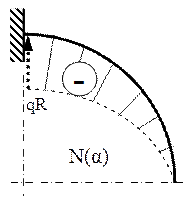
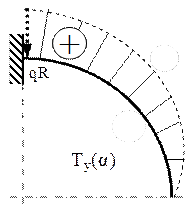
Mai precis, în cazul eforturilor de tip forţă, proiectarea încărcărilor exterioare (fig. 7.1) se face pe tangenta la axa barei din acea secţiune, pentru eforturile axiale N(α), respectiv pe direcţia normalei la axă (adică a razei cercului), pentru eforturile tăietoare T(α).
Influenţa razelor de curbură
Pentru barele a căror rază de curbură R este relativ mică (cum sunt cârligele de macarale), în raport cu înălţimea h a secţiunilor transversale (R<5h), relaţia cu care se calculează tensiunile normale – în diferitele fibre ale unei secţiuni, diferă de relaţia de la barele cotite, iar valoarea tensiunii nu mai este o funcţie liniară (ci una hiperbolică) de coordonata y a fibrei de calcul.
Astfel de bare sunt considerate „de curbură mare” şi nu fac obiectul prezentării de faţă, care se rezumă la barele „de curbură mică” sau „cu rază de curbură mare” (R≥5h), la care calculul tensiunilor se face la fel ca la barele cotite, încât condiţia de rezistenţă se scrie, în secţiunea transversală în care momentul de încovoiere are valoarea absolută maximă, astfel:
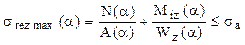 (7.1)
(7.1)
Tot pentru barele curbe există şi câteva aspecte particulare în legătură cu operaţiile de derivare şi integrare care sunt aplicate diverselor expresii ale eforturilor din secţiunile transversale.
De exemplu, dacă se ţine seama că orice element de lungime are formă curbată, se observă că variabila de integrare nu mai apare în expresii sub forma „dx”, care se întâlneşte la barele formate din segmente de dreaptă, ci sub forma elementului de curbă, adică ds = Rdα . Pe această bază se înţelege şi faptul că, pe orice regiune de pe o bară de formă circulară, relaţia diferenţială între expresiile eforturilor tăietoare şi încovoietoare se va scrie:
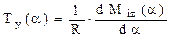 (7.2)
(7.2)

Fig. 7.1 |
Exemplele de calcul care urmează vor detalia în mod practic aspectele cele mai importante ale modului în care sunt studiate barele cu axe circulare.
Aplicaţii
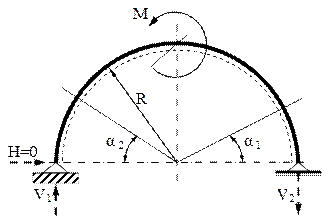
Fig. 7.2
|
7.1. Să se traseze diagramele de eforturi pentru bara în formă de semicerc solicitată ca în figura 7.1 de mai sus.
Rezolvare
Se observă că sunt mai întâi de calculat reacţiunile din reazeme (fig. 7.2), care fac ca problema să fie static determinată.
Ecuaţiile de echilibru arată că forţele V1 şi V2 sunt egale (la valoarea M/2R) şi opuse ca sens, astfel încât solicitarea barei este antisimetrică; prin urmare, cele 3 diagrame de eforturi vor respecta regulile de antisimetrie (N şi M), respectiv de simetrie (T).
Folosind împărţirea în regiuni din figură, eforturile se scriu:
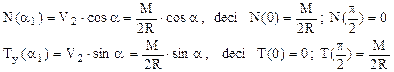
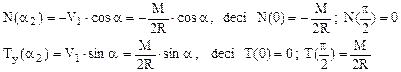
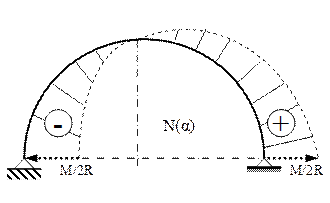 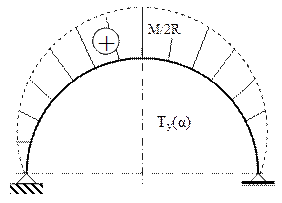
Fig. 7.3 |
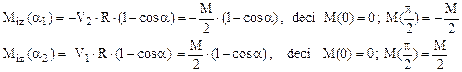
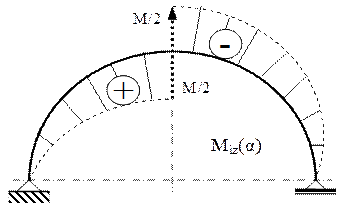
Fig. 7.4 |
Este interesant de remarcat, în legătură cu trasarea acestor diagrame, că atunci când legile de variaţie se bazează pe funcţiile sin(α) sau cos(α), valorile eforturilor cresc sau scad în mod continuu, de la o secţiune la cea vecină, încât curbele trebuie să aibă aspect de spirală (fig. 7.3-7.4).
Se observă că solicitarea periculoasă are loc în secţiunea de la mijlocul lungimii barei, unde efortul axial este nul, deci condiţia de rezistenţă se va scrie ţinând seama numai de efectele produse de încovoiere; dacă bara are secţiune pătrată, cu latura t, atunci condiţia se scrie:
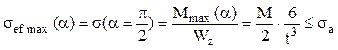
Admiţând ca material un oţel, cu rezistenţa admisibilă de 150MPa şi luând valoarea momentului exterior la nivelul de 15kNm, dimensiunea minimă a secţiunii transversale va fi:
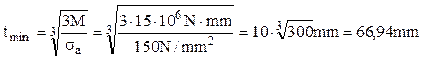
Rezultă că pătratul cu latura de 67mm este suficient, ca secţiune a barei, pentru preluarea momentului precizat mai sus. Se reaminteşte că aceste calcule sunt considerate corecte numai dacă raza de curbură a barei este de cel puţin 5 ori mai mare decât înălţimea secţiunii transversale, deci raza R în acest caz trebuie să fie măcar de 335mm lungime.
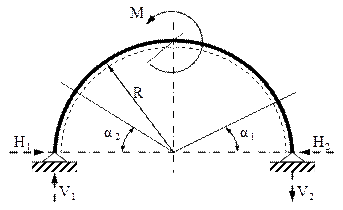
Fig. 7.5 |
7.2. Să se analizeze modul în care se schimbă solicitarea barei din aplicaţia anterioară, dacă ambele ei reazeme sunt articulaţii (fig. 7.5).
Rezolvare
Schimbarea principală este că problema devine static nedeter-minată, fiind necesar un calcul suplimentar pentru stabilirea valorii reacţiunilor orizontale. Echilibrul pe orizontală dă H1=H2=H, dar aceste forţe nu apar în ecuaţiile de momente scrise în raport cu cele două reazeme şi deci modificarea rezemării nu influenţează reacţiunile verticale:
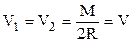
Dacă se alege rezolvarea pe baza teoremei lui Castigliano şi observând că ambele regiuni ale barei au lungimea de un sfert de cerc, expresiile eforturilor secţionale se scriu astfel:

Ecuaţia suplimentară rezultă din aplicarea teoremei, sub forma:
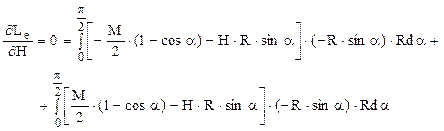
Se observă că termenii daţi de reacţiunile verticale se reduc (pentru că solicitarea este antisimetrică), astfel încât ceea ce rămâne se scrie:
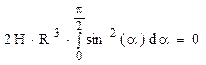
În această ecuaţie doar necunoscuta H poate fi nulă, deci soluţia este H = 0, iar acest rezultat arată, ţinând seama de expresiile de mai sus ale eforturilor secţionale de pe regiunile barei, că solicitarea nu este modificată nici într-un fel de transformarea reazemului simplu în articulaţie!
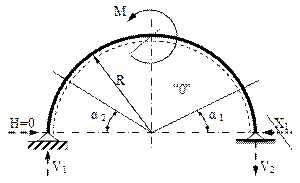 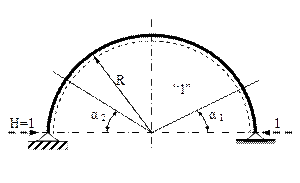
Fig. 7.6 |
Acelaşi rezultat se obţine, cum este firesc, aplicând metoda eforturilor pentru rezolvarea nedeterminării. Figura de mai jos prezintă modul în care se obţin cele două stări de încărcare fictive, cu observaţia că, dacă reazemul din dreapta este cel transformat în reazem simplu, atunci starea „0” este chiar cazul static determinat din aplicaţia 7.1.
Pe baza cunoştinţelor anterioare se poate deja înţelege că în starea „1” diagrama de momente va fi simetrică, în vreme ce starea „0” are diagrama antisimetrică, iar înmulţirea celor două diagrame, pentru a calcula valoarea coeficientului δ10, conduce la un rezultat nul!
Pentru a obţine acest lucru prin calcule, se scriu expresiile eforturilor de încovoiere din cele două stări fictive (cu precizarea că cele două regiuni ale barei sunt din nou egale ca lungimea de un sfert de cerc), astfel:
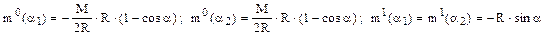
Pe această bază, pentru coeficientul menţionat se face următorul calcul:
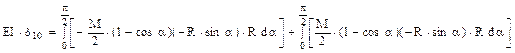
Se observă că sub integrale apar exact aceleaşi expresii, cu semne opuse, deci valoarea coeficientului va fi zero! Cunoscând că X1 = δ10/δ11 şi că δ11 este nenul, rezultă că reacţiunile orizontale sunt şi ele nule!
Dacă este necesar să se calculeze, de exemplu, deplasările secţiunii în care acţionează momentul exterior M, se remarcă mai întâi că, aşa cum s-a arătat anterior, deplasarea pe verticală din acea secţiune este nulă: starea fictivă (pentru calculul cu teorema Mohr-Maxwell) cu forţă unitară verticală pe axa de simetrie a construcţiei duce la o diagramă de momente simetrică, iar înmulţirea ei cu diagrama reală, antisimetrică, duce la rezultatul zero!
Pe de altă parte, deplasarea unghiulară (rotirea) acelei secţiuni poate fi calculată simplu aplicând teorema lui Castigliano în raport cu M, astfel:
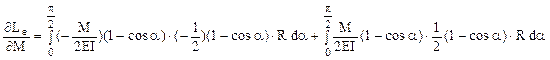
Cele două integrale sunt de fapt identice, iar calculul mai departe duce la:
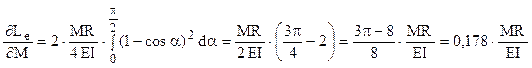
Rezultatul pozitiv arată că rotirea secţiunii din punctul cel mai de sus al barei se produce chiar în sensul momentului exterior M. Este interesant de precizat că aceste deplasări se produc atât în cazul static determinat, cât şi în cel static nedeterminat de solicitare.
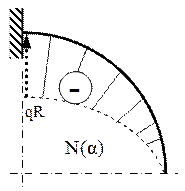
7.3. Să se dimensioneze bara în formă de trei sferturi de cerc din figura alăturată, având secţiunile transversale pătrate, cu latura t, aceeaşi pe toată lungimea, cunoscând că F=2×104N, R=0,8m, E=2×105MPa şi σa=160MPa.
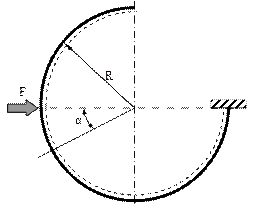
Fig. 7.7
|
Rezolvare
Problema este static determinată, iar bara are o singură regiune semnificativă, pentru că partea ei aflată deasupra forţei F este practic lipsită de solicitări.
Eforturile secţionale de pe jumătatea de cerc din partea inferioară a barei variază după următoarele expresii:
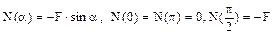
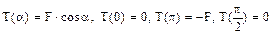
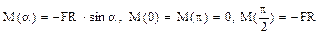
Evoluţia eforturilor pe lungimea barei este foarte uşor de urmărit, iar secţiunea periculoasă este în punctul cel mai de jos al barei, în care ambele eforturi care apar în calculul de rezistenţă ating valorile maxime. Condiţia pentru acest calcul se va scrie astfel:
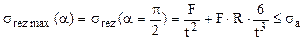
Se reaminteşte că în astfel de cazuri se face mai întâi dimensionarea numai din încovoiere, sub forma:
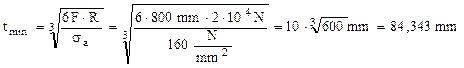
Pentru dimensionarea finală se măreşte puţin această valoare, de exemplu luând d=85mm şi se face verificarea cu relaţia exactă de mai sus:
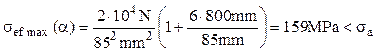
Dimensiunea adoptată este corectă.
Fig. 7.8 |
7.4. Să se stabilească modul în care se schimbă solicitarea barei din aplicaţia anterioară, atunci când în capătul de sus al barei se plasează un reazem simplu care împiedică translaţia pe orizontală.
Rezolvare
Problema devine static nedeterminată (fig. 7.8), iar cea mai convenabilă cale de rezolvare este bazată pe teorema lui Castigliano, pentru care se porneşte de la expresiile eforturilor secţionale:
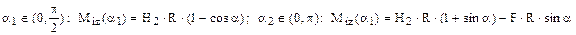
Ecuaţia suplimentară se obţine aplicând teorema în raport cu forţa H2:
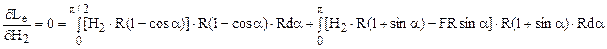
Această ecuaţie se dezvoltă astfel:
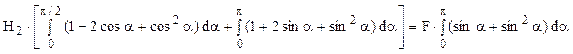
Efectuarea integralelor şi a calculelor matematice succesive conduc la următoarea valoare a reacţiunii necunoscute:
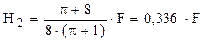
Folosind această valoare şi schema de solicitare din figura de mai sus, se stabilesc expresiile eforturilor secţionale de pe cele două regiuni ale barei:
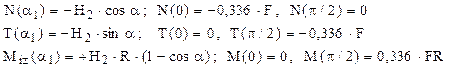
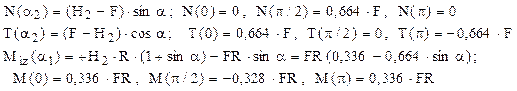
Diagramele de eforturi, trasate pe baza acestor rezultate, sunt prezentate în figurile 7.9 şi 7.10 de mai jos. Solicitarea periculoasă are loc în secţiunea din punctul cel mai de jos al barei (α2 = π/2), unde se ating valorile maxime atât pentru momentul secţional de încovoiere, cât şi pentru efortul axial.
Dimensionarea iniţială se face din încovoiere, din condiţia:
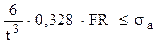
Folosind datele numerice din aplicaţia precedentă se obţine:
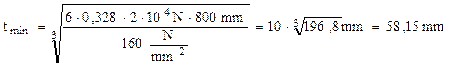
Alegem să mărim această dimensiune până la tad = 60mm, cu care se face verificarea în condiţia exactă de rezistenţă, astfel:
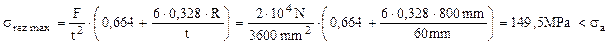
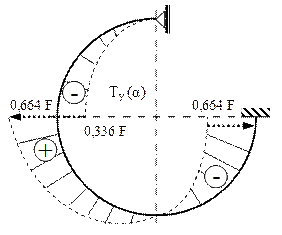 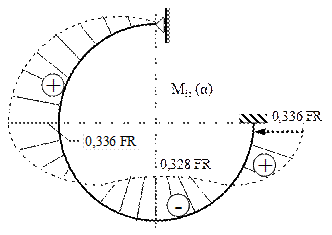
Fig. 7.9 |
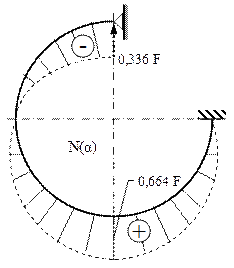
Fig. 7.10
|
Condiţia de rezistenţă este îndeplinită, deci dimensiunea adoptată mai sus este corectă. Este interesant de remarcat că introducerea reazemului simplu suplimentar a dus la uniformizarea încărcării barei, dar şi la o scădere importantă (cu două treimi din valoarea iniţială) a momentului maxim de încovoiere din bară.
Această scădere permite micşorarea ariei de material din secţiunile transversale, de un nivelul calculat astfel:
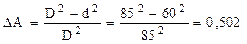
Prin urmare, consumul de material se reduce la jumătate, adică rezemarea static nedeterminată este mai eficientă economic decât situaţia iniţială; în schimb, nu trebuie neglijate dificultăţile de calcul ale variantei modificate.
Pentru exerciţiu, să ne imaginăm că se pune problema să se calculeze deplasarea pe orizontală a punctului în care acţionează forţa F, în cazul static determinat; metoda de rezolvare cea mai rapidă este cea bazată pe teorema lui Castigliano, ţinând seama că acea forţă este singura încărcare exterioară a barei, iar derivarea parţială în raport cu ea este uşor de efectuat; se reaminteşte că, pentru astfel de solicitări compuse, energia potenţială de deformare elastică provine mai ales din efectele încovoierii, iar expresia rezultată din aplicarea teoremei se scrie astfel:
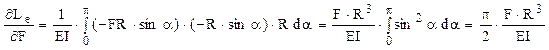
Folosind datele numerice de mai sus, deplasarea va avea valoarea:
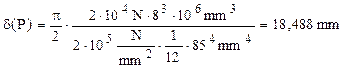
Se observă că acest rezultat este pertinent, întrucât deplasarea pe direcţia forţei reprezintă doar cu puţin mai mult de 1% din diametrul barei; în plus, este important de precizat că dimensiunile stabilite pentru secţiunea barei, în ambele variante de mai sus, se înscriu cu prisosinţă în condiţiile de definiţie pentru barele cu rază mare de curbură, deci calculele făcute au fost corecte.
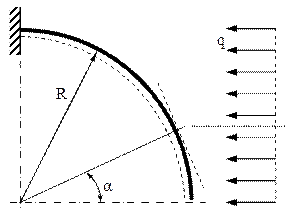
Fig. 7.11
|
Multe bare curbe din realitate sunt încărcate cu forţe care nu îşi epuizează efectele într-un singur punct, adică nu acţionează concentrat, intensitatea lor fiind repartizată pe o porţiune oarecare din lungimea axei curbe. Cele trei aplicaţii care urmează prezintă, în cea mai simplă variantă constructivă şi de rezemare (bare în consolă în lungime de un sfert de cerc), modurile posibile de acţiune a forţelor distribuite pe astfel de construcţii. Pentru fiecare caz, cerinţa problemei este de a se trasa diagramele de eforturi secţionale.
7.5. Cazul forţelor repartizate pe un segment de dreaptă (fig. 7.11), dirijat vertical sau orizontal.
Rezolvare
Rezemarea în consolă a barei face să se potrivească poziţionarea secţiunii de calcul către capătul liber. Există o singură regiune, pe toată lungimea de un sfert de cerc a barei, aşa cum se va observa în tot acest grup de aplicaţii, iar forţele secţionale se scriu:
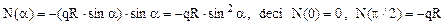
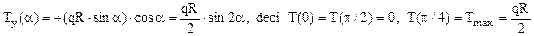
Pot fi făcute câteva sublinieri, în legătură cu stabilirea acestor expresii: mai întâi, se observă că pe porţiunea de bară de până la secţiunea de calcul apare doar o parte din forţa distribuită – cea care corespunde distanţei (R sinα) din partea inferioară a încărcării; apoi, pe lângă semnele termenilor (date de convenţiile adoptate – aceleaşi ca la barele cotite), diferenţa cea mai importantă între cele două expresii este direcţia pe care se proiectează forţele – tangenta, respectiv normala la axa barei din secţiunea (α), de unde rezultă funcţiile trigonometrice indicate mai sus.
Pentru ambele eforturi dependenţa de unghiul de poziţie este de tip sinusoidal, ceea ce permite trasarea diagramelor fără să mai fie necesar un studiu particular al funcţiilor respective (fig. 7.12).
Folosind principiile de calcul descrise mai sus, pentru eforturile secţionale de încovoiere se obţine următoarea evoluţie pe lungimea barei:
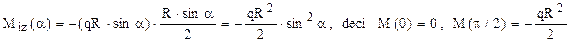
Diagramele de eforturi, trasate mai sus, arată că secţiunea periculoasă a barei este cea prinsă în reazemul încastrat, unde mărimile eforturilor coincid cu valorile reacţiunilor introduse de acel reazem şi unde se observă că atât eforturile de încovoiere, cât şi cele axiale îşi ating valorile maxime.
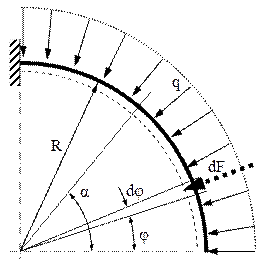
Fig. 7.13
|
7.6. Cazul forţelor repartizate pe axa barei, dirijate pe direcţia razei cercului (fig. 7.13) (normală la axă în oricare secţiune transversală).
Rezolvare
Secţionarea se face la fel ca în cazul anterior, faţă de care apare o deosebire importantă, aceea că forţele distribuite îşi schimbă direcţia de la fiecare secţiune la cea vecină. Din acest motiv efectul global al forţelor de până la secţiunea (α) trebuie calculat prin sumarea (adică integrarea) efectelor produse de forţele elementare dF; o imagine a acestora se obţine considerând unghiul intermediar φ (mai mic decât α) şi dându-i o creştere infinit mică dφ, aşa cum se arată în figură.
Forţa elementară corespunde elementului (ds = R dφ) din lungimea arcului de cerc, astfel încât vom avea că dF=qRdφ. Pentru proiectarea acestei forţe pe direcţia razei din secţiunea de calcul, se observă că unghiul dintre cele două direcţii este (α-φ) şi că integrarea trebuie efectuată în funcţie de unghiul intermediar, pe porţiunea de bară de până la secţiunea α, astfel:
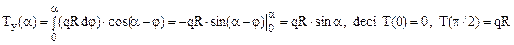
Faţă de direcţia tangentei la axa barei din secţiunea α, forţa elementară este înclinată cu unghiul complementar celui de mai sus, iar celelalte raţionamente rămân valabile în totalitate:
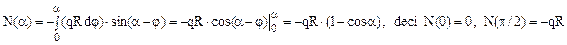
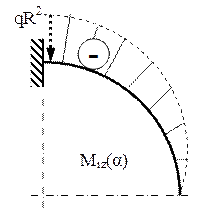
Pentru calculul momentelor secţionale este util de observat că distanţa forţei elementare până la secţiunea de calcul este [R sin(α- φ)], de unde rezultă:
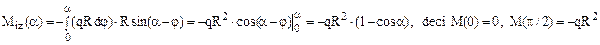
Cele trei tipuri de eforturi au evoluţii asemănătoare pe lungimea barei curbe considerate, iar diagramele lor se prezintă ca în figura următoare:
Este marcat pe diagrame faptul că „salturile” din dreptul reazemului coincid cu valorile celor trei reacţiuni pe care acel reazem le introduce asupra barei; se observă că acestea reprezintă chiar cele mai mari valori ale eforturilor secţionale, deci calculul de rezistenţă trebuie făcut exact în secţiunea din încastrare. Mai trebuie observat că, în condiţii de egalitate a intensităţii forţelor distribuite, efortul maxim de încovoiere este dublu ca mărime, dacă forţele se dirijează radial, faţă de distribuţia pe segmente de dreaptă.
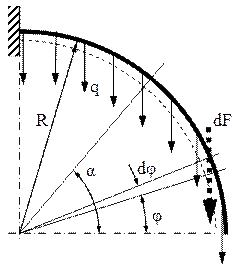
Fig. 7.15 |
7.7. Cazul forţelor repartizate pe axa barei şi dirijate pe o singură direcţie – verticală (fig. 7.15) sau orizontală.
Rezolvare
Trebuie observat că acest mod de încărcare corespunde cu felul în care acţionează asupra barelor propria lor greutate, fapt care însă nu influenţează raţionamentele ce vor fi descrise în continuare.
Se folosesc principiile de la aplicaţia anterioară, cu precizarea că în acest caz direcţia forţelor elementare este unică, ceea ce va produce anumite dificultăţi de calcul.
Pentru exemplificare, iată cum se calculează eforturile axiale din secţiunea α a barei:
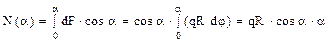
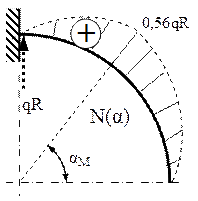
Expresiile trigonometrice de acest fel, care conţin atât argumentul α cât şi funcţii ale acestui unghi se numesc transcendente, iar rezolvarea lor necesită o atenţie specială. Se observă că valorile eforturilor axiale sunt nule, la ambele capete ale barei considerate.
Alte valori ale expresiei de mai sus, utile pentru trasarea diagramei de efort, sunt următoarele:
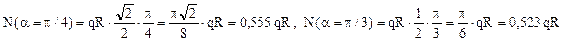
Pentru a stabili poziţia secţiunii în care N(α) este maxim, se derivează expresia de mai sus, astfel:
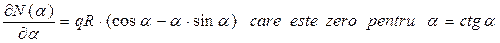
Rezolvarea acestei ecuaţii se poate face prin încercări, din aproape în aproape, găsind astfel soluţia (în radiani) αM=0,86 – adică 49,3267 grade (deci foarte aproape de mijlocul lungimii barei). Cu această valoare se calculează efortul axial maxim de pe bară:
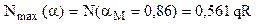
Analog se studiază evoluţia eforturilor tăietoare din secţiunile transversale:
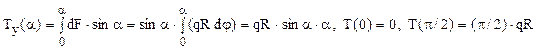
Această funcţie este strict crescătoare pe intervalul de definiţie din această problemă, deci pentru trasarea diagramei este suficient să fie cunoscute valorile din secţiunile de la capetele barei.
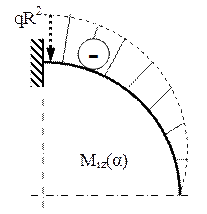
Pentru stabilirea expresiei eforturilor de încovoiere, se observă că distanţa forţei elementare faţă de secţiunea de calcul se măsoară cel mai simplu pe axa orizontală de la care începe măsurarea unghiului de poziţie: ea este diferenţa între catetele orizontale ale triunghiurilor dreptunghice construite pe raza R, la unghiurile α, respectiv φ:
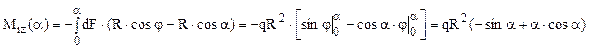
Se observă că derivata acestei expresii coincide cu expresia eforturilor tăietoare de mai sus (cu semn schimbat, pentru că s-a calculat din dreapta faţă de secţiunea α), de unde rezultă că evoluţia momentelor de încovoiere este monotonă (în acest caz – descrescătoare) şi că singurul punct de extrem este în capătul liber al barei (unde α=0), unde forţa tăietoare se anulează.
Pentru trasarea diagramei mai sunt necesare valorile expresiei la capetele intervalului de definiţie, iar acestea sunt: M(0)=0 , M(π/2)=-qR2 .
Este remarcabilă asemănarea diagramelor T(α) şi M(α) cu cele de la forţele distribuite radial, în vreme ce eforturile axiale au o evoluţie specifică. Cea mai mare solicitare de încovoiere are loc în secţiunea din încastrare, pentru care se face calculul de rezistenţă, după care este bine să se facă o verificare a dimensiunii astfel obţinute, scriind condiţia (7.1) pentru secţiunea (αM), în care N(α) atinge valoarea maximă.
Aplicaţia care urmează are ca obiect o bară curbă închisă, frecvent folosită în practică, de exemplu sub formă de inele dinamometrice – dispozitive pentru măsurarea forţelor, bazate pe proporţionalitatea dintre alungirea lor diametrală şi valoarea încărcărilor F care le solicită.
7.8. Pentru inelul construit şi solicitat ca înfigura de mai jos, să se traseze diagramele de eforturi, să se scrie relaţia tensiunii rezultante maxime şi să se calculeze cu cât se modifică, sub acţiunea celor două forţe concentrate, lungimea diametrelor de pe orizontală, respectiv verticală.

Fig. 7.17 |
Rezolvare
Este mai întâi de remarcat faptul că acest inel nu are nevoie de rezemare, întrucât se află în echilibru stabil sub acţiunea celor două forţe concentrate care îl încarcă. Pe de altă parte se observă că, bara având conturul închis, avem de-a face cu o triplă nedeterminare statică interioară.
Solicitarea inelului este simetrică, deci secţionarea lui cea mai avantajoasă se face pe una dintre axele de simetrie. Alegem axa verticală şi constatăm că efortul tăietor din cele două secţiuni astfel obţinute are valoarea zero şi mai trebuie figurate efortul axial şi cel de încovoiere, ambele cu valori egale între ele şi la fel orientate în cele două tăieturi imaginare simetrice (fig. 7.18).
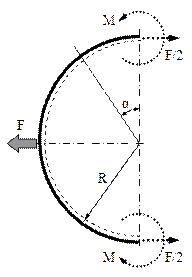
Fig. 7.18 |
Specificul construcţiilor care au două axe de simetrie (inclusiv pentru solicitările lor) este că din ecuaţia de echilibru pe orizontală, scrisă pentru forţele de pe această jumătate de bară, se poate calcula efortul axial necunoscut, egal cu jumătate din forţa F. Problema rămâne astfel cu o singură necunoscută static nedeterminată – efortul de încovoiere M.
Partea de bară astfel construită fiind şi ea simetrică şi având solicitări simetrice, putem opta să analizăm eforturile secţionale pe o jumătate a ei; trebuie menţionat că este necesar ca, pentru a evita introducerea unor necunoscute noi, în noua secţiune, făcută pe direcţia axei orizontale de simetrie a inelului iniţial, să fie introdus un reazem încastrat imaginar (fig. 7.19); acest lucru nu contrazice modul în care inelul se deformează, întrucât (aşa cum s-a arătat anterior) în secţiunile de pe axele lui de simetrie nu se produc rotiri!
Cea mai simplă cale pentru rezolvarea nedeterminării pe acest sfert de inel este bazată pe metoda eforturilor, pentru care cele două stări fictive de încărcare sunt reprezentate în figura 7.19, inclusiv modul în care se face secţionarea lor. Pentru ambele situaţii există pe toată lungimea barei rămase o singură regiune (cu unghiul de poziţie cuprins între 0 şi π/2), iar expresiile eforturilor de încovoiere se scriu astfel:
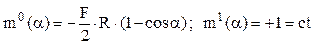
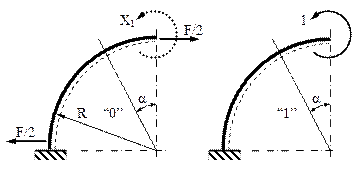
Fig. 7.19 |
Cei doi coeficienţi care vor completa ecuaţia metodei se calculează analitic, astfel:
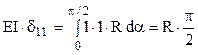
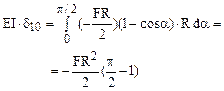
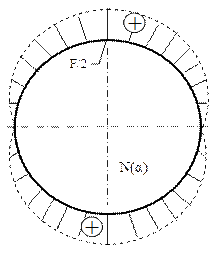
Fig. 7.20 |
Cu aceste rezultate se obţine că momentul necunoscut are valoarea:
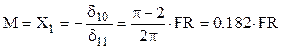
Introducând această mărime pe schiţa de mai sus a stării fictive „0”, expresiile eforturilor secţionale pentru un sfert din inelul real sunt:
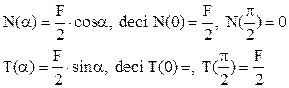
Procedând analog se stabilesc eforturile de încovoiere din secţiunile inelului, astfel:

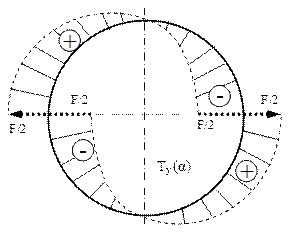 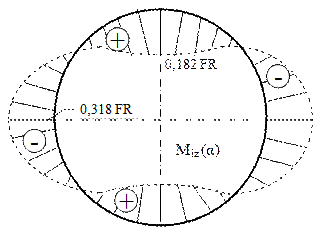
Fig. 7.21 |
Folosind expresiile şi valorile scrise mai sus, s-au trasat diagramele de eforturi din figurile 7.20 şi 7.21, care arată că cea mai periculoasă solcitare a inelului (dinamometric) se produce chiar în secţiunile în care acţionează cele două forţe concentrate, unde se face şi calculul de rezistenţă.
Relaţia tensiunii rezultante maxime se scrie sub forma (7.1), iar dacă se admite că secţiunea transversală a inelului este pătrată cu latura t rezultă:
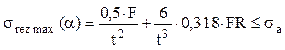
Pentru aflarea deformaţiilor inelului, pe direcţiile diametrelor orizontal, respectiv vertical, sunt de subliniat două aspecte importante ale acestui tip de problemă:
- mai întâi, fiind vorba despre două forţe F aplicate simetric, metodele de calcul aplicate pentru ambele forţe simultan (cum se va vedea mai jos) duc la găsirea deplasărilor sumate ale punctelor lor de aplicare (adică direct a deformaţiilor diametrale!);
- în al doilea rând, s-a arătat anterior că, la calculul cu teorema Mohr-Maxwell a deplasărilor în cazul construcţiilor static nedeterminate, se înmulţeşte starea reală de solicitare cu starea fictivă aplicată unui sistem de bază, convenabil ales, al construcţiei; această metodă se va folosi în cele ce urmează.
Pentru calculul deformaţiei la capetele diametrului orizontal AB, o variantă simplă de sistem de bază este cel în care inelul este secţionat imaginar în secţiunea inferioară de pe diametrul vertical (fig. 7.22).
Fig. 7.22 |
Acest model de solicitare simetrică produce eforturi de încovoiere numai pe cele două regiuni – şi ele simetrice – din jumătatea superioară a construcţiei, cu o evoluţie dată de relaţia:
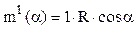
Utilizând ultima formă a expresiei de mai sus a efortului de încovoiere Miz(α) de pe inelul real, deformaţia (alungirea) diametrului AB se calculează astfel (cu teorema Mohr-Maxwell):
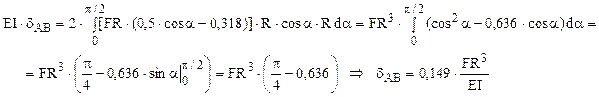
În mod analog se fac calculele pentru deformaţia diametrului vertical CD, pentru care sistemul de bază se studiază simplu, dacă este ales similar celui de mai sus, dar rotit cu 90°, în sens trigonometric (fig. 7.23); apar din nou doar două regiuni, simetrice, pe jumătatea din stânga a inelului, pe care există eforturi secţionale de încovoiere, având următoarea lege de variaţie:
Fig. 7.23 |

Teorema Mohr-Maxwell se aplică astfel:
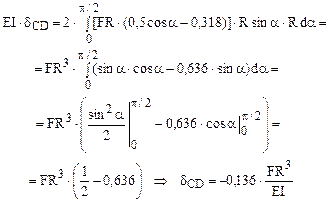
Valorile astfel obţinute pentru deformaţiile inelului studiat se folosesc la etalonarea dispozitivelor pentru măsurarea forţelor.
Ca metodă alternativă, deformaţia de pe diametrul orizontal AB poate fi calculată direct, pe baza expresiei eforturilor secţionale de încovoiere de pe inelul real, folosind teorema lui Castigliano în raport cu forţele F:
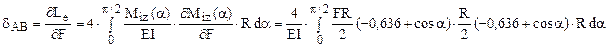
După efectuarea calculelor matematice, se ajunge la acelaşi rezultat ca mai sus, δAB = 0,149 FR3/EI . Trebuie semnalat că această metodă necesită calcule mai laborioase decât aplicarea teoremei Mohr-Maxwell şi că este potrivită doar pentru stabilirea deformaţiei de pe direcţia forţelor F.