 Fig. 9.1 |
Această categorie de corpuri solide include o gamă largă de aplicaţii inginereşti, de la rezervoarele pentru transportul şi depozitarea materialelor fluide sau pulverulente, până la cupole şi părţi componente ale aparatelor de zbor. Structura acestor corpuri seamănă cu a plăcilor curbe, de grosime mică, iar forma le este definită de suprafaţa lor mediană, care ia naştere prin rotirea unei curbe oarecare (numită generatoare) în jurul unei axe, pe care o întâlneşte sau nu şi care reprezintă axa vasului.
 Fig. 9.1 |
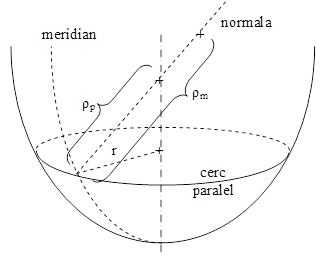
Pe astfel de suprafeţe pot să fie definite, în orice punct, raze de curbură în număr infinit, diferite ca valori în funcţie de planul în care sunt măsurate. Valorile principale ale acestei mulţimi se definesc pe normala dusă la suprafaţa curbă, în acel punct (fig. 9.1) şi sunt legate de două familii de curbe, denumite (în analogie cu globul pământesc) meridiane şi respectiv cercuri paralele (cu razele notate cu r).
Cele două raze de curbură principale dintr-un punct arbitrar al vasului, identificat prin distanţa x a secţiunii (perpendiculare pe axa vasului) în care se află (faţă de un reper de pe axă, convenabil ales), sunt notate cu indicele uneia dintre aceste familii de curbe şi se definesc astfel:
Din faptul că vasele despre care se discută aici au pereţi subţiri, în comparaţie cu distanţele de la suprafaţa vasului până la axa de rotaţie, se deduc două consecinţe importante: pe de o parte, devine admisibilă ipoteza că tensiunile care apar în pereţi, într-un punct arbitrar, sunt constante ca mărime pe grosimea acestora, iar pe de altă parte starea de tensiuni din orice punct din pereţii vasului este plană, cu tensiunile principale dirijate tangent la cele două familii de curbe prezentate mai sus. Este important de semnalat că prin fiecare punct al vasului trec două astfel de curbe, una de tip meridian şi un cerc paralel, ale căror tangente sunt mereu reciproc perpendiculare.
Pe această bază s-a ajuns ca tensiunile principale din orice punct să fie definite şi notate tot în conexiune cu meridianele şi paralelele vasului, adică σm(x), respectiv σp(x) (cum se prezintă în figura 9.2, pe un element de volum izolat imaginar din peretele, de grosime h, al vasului).
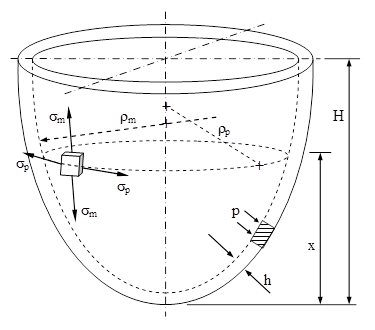 Fig. 9.2 |
Tot pe baza faptului că pereţii sunt subţiri se admite că, deşi de obicei sunt din oţel sau din alte materiale rezistente, aceştia se comportă, sub solicitări mecanice, după modelul unei membrane: preiau tensiuni de întindere, dar nu suportă încovoiere. Prin urmare, în orice punct al vasului se pot măsura, pe direcţii diferite, o infinitate de valori ale tensiunilor, toate de întindere; iar cele extreme au direcţii tangente la cercul paralel, respectiv la curba meridian din acel punct.
Pentru început se ia în considerare solicitarea vasului prin presiunea p, exercitată asupra pereţilor de fluidul din vas; când acesta este un gaz (a cărui greutate e neglijabilă faţă de efectele presiunii, la fel ca greutatea vasului în sine!), presiunea are valoare constantă în toate punctele vasului.
Dacă punctul în care se face analiza se află în secţiunea transversală situată la distanţa x faţă de reper (în figura alăturată reperul este capătul de jos al vasului), atunci între valorile tensiunilor principale şi parametrii vasului din acel punct este adevărată următoarea relaţie:
![]() (9.1)
(9.1)
Aceasta este ecuaţia lui Laplace, matematicianul francez care a dedus-o cel dintâi, cu ea se începe studiul oricărui vas cu pereţi subţiri; necunoscutele din ecuaţie sunt tensiunile din punctul de calcul, iar găsirea acestor valori necesită o a doua relaţie care să le conţină.
Scrierea ecuaţiei a doua se poate explica direct pentru cazul cel mai general de încărcare a unui vas de revoluţie cu pereţi subţiri, cel în care conţinutul este o pulbere sau un fluid cu greutate proprie importantă şi care solicită pereţii vasului cu o presiune care creşte, de la suprafaţa de sus a încărcăturii către baza ei. Se face din nou precizarea că, grosimea pereţilor fiind mică, greutatea vasului este neglijabilă, în raport cu solicitările exterioare, astfel încât nu este inclusă în calculul de rezistenţă.
Mai trebuie subliniat că, pentru a se ajunge la o solicitare simetrică a pereţilor (cu p(x) = ct în orice secţiune transversală!), acest tip de încărcare necesită poziţionarea vasului cu axa verticală, cerinţă care este respectată în majoritatea aplicaţiilor practice din această categorie.
În condiţiile descrise, eforturile (toate de tip forţă!) care apar în pereţii vasului, într-o secţiune transversală oarecare, notată cu (x), exprimă efectele produse de trei tipuri de mărimi fizice (două exterioare, active şi una interioară, reactivă):
Folosind aceste notaţii, ecuaţia a doua pentru stabilirea tensiunilor, la vasele de revoluţie cu pereţi subţiri, exprimă echilibrul forţelor de mai sus, proiectate pe direcţia axei de rotaţie a vasului, astfel:
![]() (9.2)
(9.2)
Ecuaţiile (9.1) şi (9.2), particularizate cu parametrii concreţi ai unei aplicaţii date, sunt suficiente (problema este static determinată!) pentru găsirea expresiilor după care variază cele două feluri de tensiuni pe înălţimea vasului (adică în funcţie de poziţia secţiunii transversale de calcul).
Trasarea diagramelor care exprimă aceste evoluţii evidenţiază în ce secţiune se produce solicitatea periculoasă în pereţii vasului, iar valorile tensiunilor din acea secţiune se vor folosi în calculul de rezistenţă. Se poate recunoaşte o stare plană de solicitare, cu tensiunile principale σm(x) şi σp(x), al căror efect global trebuie evaluat cu una dintre teoriile de rupere.
Ca principiu ar trebui folosită teoria εmax, pentru materialele fragile, respectiv una dintre teoriile τmax şi Uf, dacă materialul vasului este tenace; pe de altă parte este util de observat că, deoarece tensiunile principale au acelaşi semn, teoria τmax conduce la aceeaşi valoare a tensiunii echivalente ca şi teoria σmax (întrucât σ3 = 0), adică egală cu cea mai mare dintre tensiunile principale. Această variantă este preferată pentru multe aplicaţii inginereşti, astfel că relaţia calculului de rezistenţă se scrie:
![]() (9.3)
(9.3)
Pe baza acestei relaţii se pot rezolva probleme din toate cele trei categorii clasice întâlnite în studiul rezistenţei materialelor:
a. de verificare – cunoscând toţi parametrii constructivi şi de încărcare, trebuie stabilit dacă proiectarea vasului este corectă;
b. de încărcare maximă – se calculează cât de mult fluid poate fi introdus într-un vas complet cunoscut, ca dimensiuni şi ca material;
c. de dimensionare – se cunosc materialul vasului şi încărcătura care trebuie preluată, dar şi o parte dintre dimensiunile finale; de exemplu se impun înălţimea H şi raza R, pentru care se stabileşte grosimea necesară hmin a tablei din care trebuie realizat vasul, sau se impun H şi h şi se calculează valoarea maximă Rmax a razei pe care vasul o poate avea.
Aplicaţii
9.1. Calculul conductelor care transportă fluide sub presiune
Cele mai importante utilizări inginereşti le au conductele din instalaţiile comandate prin circuite hidraulice sau pneumatice; acestea au, de regulă, diametre mici, dar presiuni mari în fluid, încât calculul lor trebuie realizat în mod cât mai precis şi atent.
Din faptul că fluidul circulă liber prin aceste conducte rezultă, pe de o parte, că presiunea este constantă p(x) = p în orice punct al lor, iar pe de altă parte că pereţii conductelor nu sunt solicitaţi pe direcţie longitudinală, adică tensiunile σm(x) sunt nule în toate punctele pereţilor. Prin urmare, tensiunile de calcul vor fi cele circumferenţiale σp(x), iar pentru găsirea valorii lor este suficient să se particularizeze ecuaţia lui Laplace (9.1), pentru conducta studiată.
În condiţiile descrise şi observând forma cilindrică a conductelor, cu pereţi de grosime h şi rază R (din care rezultă că ρp(x) = ct = R), ecuaţia lui Laplace conduce la relaţia calculului de rezistenţă, astfel:
![]() (9.4)
(9.4)
Observaţie: Întrucât valorile presiunii din relaţiile de calcul vor fi exprimate de obicei în MPa, este important să fie reamintit că presiunea exprimată în atmosfere se transformă în MPa folosind egalitatea 1atm = 0,1MPa.
Ca exemplu de calcul, se consideră situaţia în care trebuie stabilit ce presiune maximă pmax poate să suporte o conductă, făcută dintr-un oţel cu rezistenţa admisibilă la tracţiune σa = 180MPa, pentru următoarele variante de dimensiuni:
a. R = 3mm, h = 1mm
![]()
b. R = 3mm, h = 0,5mm
![]()
c. R = 2mm, h = 1mm
![]()
d. R = 2mm, h = 0,5mm
![]()
e. R = 1,5mm, h = 0,5mm
![]()
f. R = 1mm, h = 0,25mm
![]()
Concluzia importantă la care se ajunge este că astfel de conducte suportă presiuni de valori importante, în condiţiile unor dimensiuni transversale foarte mici, apropiate de cele ale conductorilor electrici din care se compun circuitele clasice de comandă pentru diverse instalaţii industriale.
9.2. Calculul vaselor care conţin gaze sub presiune
După cum s-a arătat deja, particularitatea principală a aceste vase constă în greutatea cu totul neglijabilă a gazelor, ceea ce simplifică mult ecuaţia a doua, dar face şi ca presiunea să fie constantă în orice punct din vas.
Principiile de calcul pot fi exersate într-un mod unitar dacă se imaginează un vas format din tronsoane având geometrii distincte (fig. 9.3), de tipurile cel mai des întâlnite în practica inginerească.
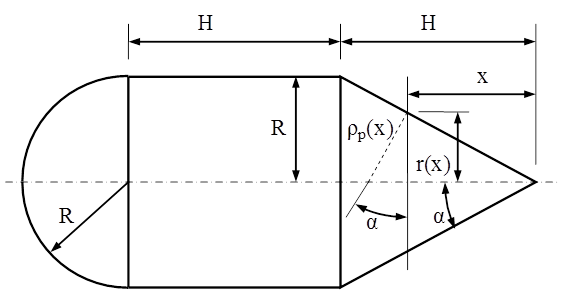 Fig. 9.3 |
Se poate observa că, în cazul vaselor cu gaze, simetria de solicitare este asigurată chiar şi la aşezarea orizontală a axei de rotaţie; în plus, pentru vasele cilindrice şi sferice nu există deosebiri între secţiunile transversale, deci calculul este identic oriunde ar fi făcută secţionarea acelui vas, ceea ce nu mai este valabil la vasele de formă conică.
Particularităţile celor trei tronsoane vor fi evidenţiate prin analiza lor succesivă:
a. porţiunea sferică are proprietatea unică de egalitate a razelor principale de curbură, în orice punct, adică ρp(x) = ρm(x) = R; pe de altă parte, simetria specială a sferei şi presiunea constantă din interior fac ca tensiunea din perete să aibă o valoare unică, indiferent de direcţia pe care s-ar măsura, deci σp(x) = σm(x) = σ; din aceste motive, ecuaţia lui Laplace (9.1) se scrie simplu şi este suficientă pentru aflarea valorii tensiunilor principale, cu care se completează condiţia de rezistenţă de pe acest tronson al vasului:
![]()
Prin urmare, un vas sferic cu gaz sub presiune are aceeaşi valoare a tensiunii, în orice punct şi pe orice direcţie s-ar face măsurarea, ceea ce este uşor de intuit dacă se imaginează orice minge (din cauciuc) umplută cu aer.
b. porţiunea cilindrică are ca generatoare o dreaptă, de unde ρm(x) = ∞, în vreme ce a doua rază de curbură principală este ρp(x) = R; aceste date fac ca ecuaţia lui Laplace să se scrie astfel:
![]()
Pentru scrierea ecuaţiei a doua trebuie observat că termenul dat de greutatea fluidului va lipsi complet, că generatoarea vasului este paralelă cu axa de rotaţie (adică înclinarea tensiunilor σm va fi α = 0, de unde cosα = 1), că aria de fluid din orice secţiune este Af(x) = πR2 şi că aria de metal din secţiunea (x) este de formă inelară, cu pereţi subţiri; o astfel de arie se exprimă simplu dacă se imaginează că inelul este decupat, pe direcţia unei raze, apoi desfăşurat pe un plan, încât se obţine un dreptunghi îngust, cu înălţimea h şi cealaltă latură egală cu lungimea pe contur (2πR) a inelului iniţial; prin urmare Am(x) = 2πRh.
Folosind aceste informaţii, precum şi toate datele iniţiale din problemă (de exemplu aceea că presiunea are peste tot valoarea p), ecuaţia (9.2) se reduce la următoarea egalitate:
![]()
Valorile celor două tensiuni principale obţinute mai sus nu depind de poziţia (x) a secţiunii de calcul, ceea ce confirmă că nici în cazul vaselor cilindrice cu gaze nu există deosebiri de calcul între secţiunile transversale. În plus, s-a obţinut rezultatul remarcabil că tensiunile meridiane au valori pe jumătate faţă de celelalte tensiuni principale din pereţii vasului; aceasta arată că astfel de vase sunt puse în pericol de tensiunile circumferenţiale şi că eventuala lor fisurare se va produce pe direcţia generatoarei (perpendiculară pe cea a tensiunilor periculoase).
Relaţia calculului de rezistenţă se scrie astfel:
![]()
Comparând cu rezultatele de la porţiunea sferică, se observă că tensiunile de pe tronsonul cilindric sunt de două ori mai mari, adică un vas sferic este mai avantajos, întrucât suportă presiuni de gaz duble, faţă de un vas cilindric din acelaşi material şi cu aceleaşi valori ale parametrilor R şi h.
Trebuie însă subliniat că superioritatea vaselor sferice este greu de exploatat în practică, datorită problemelor dificile de rezemare puse de aceste vase şi care nu există pentru cele cilindrice.
c. porţiunea conică are tot generatoare dreaptă, cu ρm(x) = ∞, iar a doua rază de curbură principală este variabilă ca mărime, de la o secţiune transversală la alta, întrucât depinde de raza r(x) a secţiunii şi de înclinarea generatoarei, după relaţia ρp(x) = r(x)/cosα; ecuaţia lui Laplace are forma:
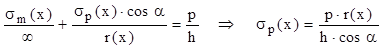
Acest rezultat, împreună cu desenul de mai sus (fig. 9.3), arată că tensiunile circumferenţiale de la vasul conic cu gaz variază liniar pe înălţimea vasului, la fel cu raza r(x), adică sunt nule la vârful conului şi maxime la baza lui, unde valoarea lor este:
![]()
Pentru completarea ecuaţiei (9.2) se folosesc raţionamentele făcute pentru tronsonul cilindric, ţinând însă seama că raza secţiunii este variabilă şi că generatoarea este înclinată:
![]()
Tensiunile cele mai mari sunt cele circumferenţiale, astfel încât condiţia de rezistenţă se scrie sub forma:
![]()
Rezultă că şi pe tronsoanele conice fisurarea tinde să se producă tot pe direcţia generatoarei vasului care conţine gaz sub presiune. În plus, valoarea tensiunilor maxime din porţiunea conică diferă de cea de la cilindru doar prin mărimea cosα, care apare la numitor (deci tensiunile din zona conică sunt cele mai mari din întregul vas!).
O consecinţă importantă a acestei diferenţe este că, la graniţa dintre cele două tronsoane, se produce un salt al tensiunilor, care poate fi periculos pentru integritatea vasului. În mod obişnuit se adoptă, în faza de proiectare, o măsură de consolidare locală a pereţilor, prin adăugarea unor bandaje exterioare, solidarizate cu vasul, pentru a mări grosimea h în zona saltului.
Analiza condiţiilor de rezistenţă scrise mai sus arată că tensiunile din pereţi, la vasele cu gaze sunt cu atât mai mari cu cât presiunea gazului şi raza R sunt mai mari, dar sunt invers proporţionale cu grosimea pereţilor; cota H are influenţă doar la vasele conice, unde creşterea înălţimii duce la scăderea înclinării α şi la creşterea lui cosα, deci la scăderea tensiunilor.
În principiu se observă că vasele de dimensiuni mari suportă doar presiuni relativ mici ale gazelor conţinute. De exemplu, se propune a se calcula ce presiune maximă de gaz suportă un vas conic cu H=1m şi α=60°, făcut din tablă de oţel cu grosimea h=3mm şi rezistenţa admisibilă la tracţiune σa=160MPa.
Relaţia de rezistenţă conduce la următoarele calcule:
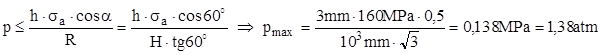
Rezultă că, deşi este destul de rigid, vasul propus poate suporta, pentru gazul pe care îl conţine, doar ceva mai mult decât presiunea atmosferică.
Pentru a evidenţia diferenţa de capabilitate dintre vasele cilindrice şi conice, construite în parametri asemănători, se va compara presiunea maximă pe care o pot suporta două astfel de vase, făcute din oţel cu σa = 160MPa şi având H = R = 0,4m; h = 2mm.
Din condiţiile de rezistenţă scrise mai sus pentru cele două feluri de vase rezultă că pmax con = pmax cil·cosα , iar pentru vasul cilindric relaţia presiunii admisibile conduce la:
![]()
Deoarece H = R, înseamnă că (semi)unghiul la vârf al conului este α = 45° şi rezultă că:
![]()
Cu cât conul are unghiul de la vârf mai mare, cu atât vasul conic va putea prelua o fracţie mai mică din presiunea permisă pentru vasul cilindric.
9.3. Calculul vaselor care conţin lichide
După cum s-a arătat anterior, principala particularitate în acest tip de solicitare este că presiunea din vas este variabilă, fiind proporţională cu înălţimea coloanei de lichid aflată deasupra secţiunii de calcul. Diferenţe notabile apar în calcule în funcţie de forma vasului, de modul în care este rezemat şi de nivelul până la care se află introdus lichid în vas.
|
A. Vase cilindrice rezemate la bază
Specificul acestei rezemări este apariţia la baza vasului (fig. 9.4) a reacţiunii R , egală ca mărime cu greutatea lichidului din vas. Celelalte elemente necesare pentru calculul tensiunilor din pereţii vasului au fost deja discutate şi vor fi folosite în cele de mai jos.
Ecuaţia lui Laplace se scrie ca la vasele cu gaze:
![]()
Trebuie observat că, la vasele cilindrice, este util ca poziţia x a secţiunii transversale de calcul să fie indicată în raport cu nivelul superior al lichidului din vas, aşa cum se observă în figură. În acest fel, presiunea din zona cu lichid (care în cazul de faţă ocupă trei sferturi din înălţimea vasului) se exprimă sub forma p(x)=γx, iar expresia şi valorile importante ale tensiunilor circumferenţiale se vor scrie astfel:
![]()
Pentru regiunea din partea de sus a vasului, în care nu există lichid, pereţii nu sunt încărcaţi cu presiune, deci membrul drept din ecuaţia lui Laplace este nul şi se obţine că σp(x1) = 0 , aşa cum este arătat şi pe grafic.
Analiza tensiunilor σm(x) necesită scrierea ecuaţiei a doua, de forma (9.2), care pentru vasul de faţă are următorul aspect:
![]()
Ariile Am(x) şi Af(x) au fost explicitate şi se scriu la fel ca în aplicaţia anterioară, iar rezultanta R este egală cu greutatea lichidului din vas:
R, = γ·πR2·(3H/4)
În fine, presiunea p(x) şi volumul V(x) – al lichidului de sub secţiune sunt diferite pentru cele două regiuni marcate pe înălţimea vasului şi pe care ecuaţia de mai sus se particularizează astfel:
- pentru x1 € (0; H/4) (regiunea lipsită de lichid)
p(x1) = 0 Vf(x1) = πR2·(3H/4)
![]()
termenii din membrul drept al acestei ecuaţii se reduc, deci σm(x1) = 0;
- pentru x2 € (0; 3H/4) (regiunea care conţine lichid)
p(x2) = γ·x Vf(x1) = πR2·[(3H/4)-x]
![]()
la fel ca mai sus, membrul drept este nul, deci σm(x2) = 0.
Concluzia acestei aplicaţii este că la vasele cilindrice cu lichide care sunt rezemate la bază tensiunile de pe direcţia meridiană sunt nule pe toată înălţimea vasului, indiferent dacă acesta este umplut complet sau parţial!
Pereţii sunt solicitaţi numai prin tensiunile circumferenţiale, care sunt proporţionale cu presiunea din vas, adică există numai în zona care conţine lichid; presiunea fiind crescătoare odată cu adâncimea în lichid, tensiunile sunt maxime la fundul vasului (unde se formează prima fisură, pe direcţie verticală, dacă vasul nu este bine proiectat), iar relaţia calculului de rezistenţă se va scrie ca la o stare uniaxială de tensiuni:
![]()
Exemplu numeric: se proiectează un rezervor pentru apă (având greutatea specifică γ=104N/m3=10-5N/mm3) din tablă de oţel cu σa = 160MPa, rezemat pe sol la partea de jos şi având dimensiunile globale R = 8m şi H = 5m. Să se calculeze grosimea minimă a tablei care va trebui folosită.
Rezolvare: condiţia de rezistenţă dă relaţia grosimii minime
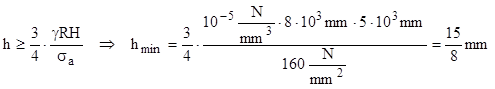
Tabla groasă de doar 2mm este suficientă pentru realizarea rezervorului.
B. Vase cilindrice rezemate pe circumferinţa superioară
Acest mod de rezemare face ca reacţiunea să apară la partea de sus şi să nu influenţeze tensiunile din pereţi, astfel încât valorile σm(x) nu mai sunt nule pe nici o zonă a vasului. Există însă deosebiri de abordare între vasele care sunt umplute parţial, respectiv complet cu lichid, cea mai importantă fiind separarea a două regiuni, pe înălţimea vasului, în loc de una singură.
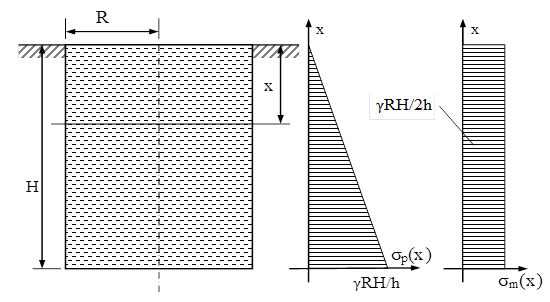 Fig. 9.5 |
Pe de altă parte, cele două ecuaţii de echilibru se scriu la fel ca în cazul studiat anterior, aşa cum se va arăta în continuare.
B1. cu umplere completă
Din ecuaţia lui Laplace rezultă tensiunile circumferenţiale:
![]()
Ecuaţia a doua se particularizează astfel:
![]()
Se obţine deci că la acest vas tensiunile de pe meridiane sunt constante, pe toată înălţimea vasului, la valoarea: σm(x) = (1/2)(γRH/h) = (1/2)σp max
Prin urmare, condiţia de rezistenţă pentru acest vas se va scrie:
![]()
Pentru a observa ordinul de mărime al dimensiunilor unui astfel de vas, vom calcula grosimea minimă necesară a tablei de oţel, cu σa = 160MPa, din care trebuie construit un vas, rezemat pe conturul superior, cu R = 3m şi H = 4m, care va fi umplut complet cu apă.
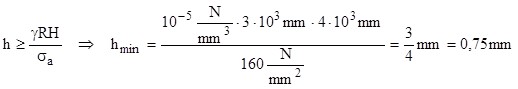
Se observă că tabla de nici măcar 1mm grosime este suficientă pentru realizarea vasului studiat.
B2. cu umplere parţială
|
Urmărind elementele caracteristice de pe cele două regiuni ale vasului, cele două ecuaţii de echilibru se particularizează astfel:
- pentru x1 € (0; H/4) (regiunea lipsită de lichid)
p(x1) = 0 , deci σp(x1) = 0 , iar Vf(x1) = πR2·(3H/4)
![]()
- pentru x2 € (0; 3H/4) (regiunea care conţine lichid)
p(x2)=γ·x ![]()
În ecuaţia a doua apare volumul de lichid de sub secţiune, având expresia Vf(x2) = πR2·[(3H/4)-x], iar ecuaţia se scrie astfel:
![]()
Folosind aceste rezultate se trasează diagramele celor două categorii de tensiuni, aşa cum se arată în figura de mai sus. Este interesant de observat că valoarea cea mai mare a tensiunilor, ca şi condiţia de rezistenţă, se scriu exact la fel ca la vasul aşezat pe suprafaţa lui inferioară.
Mai există o concluzie comună tuturor vaselor cilindrice cu lichid: solicitarea lor periculoasă are loc, indiferent de felul rezemării, în secţiunea de la baza vasului, iar fisurarea tinde să se producă pe direcţia generatoarei.
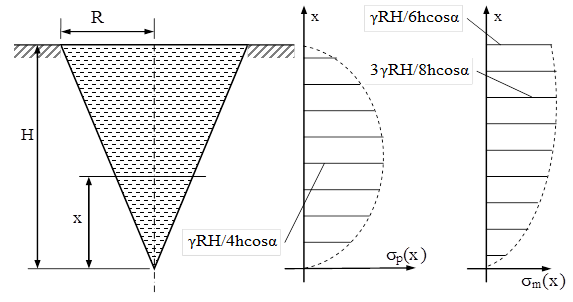 Fig. 9.7 |
C. Vase conice rezemate pe circumferinţa superioară
Este uşor de observat că parametrii solicitării nu se modifică, pe toată înălţimea vasului, deci nu este necesară divizarea acesteia în mai multe regiuni; la fel ca la vasul conic cu gaz, generatoarea este o dreaptă, deci ρm(x) = ∞, în vreme ce a doua rază de curbură principală este variabilă ca mărime, de la o secţiune la alta, întrucât depinde de raza r(x) a secţiunii şi de înclinarea generatoarei, după relaţia ρp(x) = r(x)/cosα (a se revedea fig. 9.3).
Trebuie subliniat că, pentru ca r(x) să fie proporţional cu poziţia x a secţiunii, este avantajos ca această distanţă să fie măsurată faţă de vârful conului (cum se arată în fig. 9.7), iar ecuaţia lui Laplace are forma:
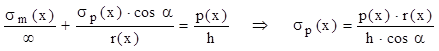
Presiunea se exprimă simplu, ţinând seama de înălţimea coloanei de lichid care se află deasupra secţiunii (x), adică p(x) = γ (H-x), iar raza secţiunii se poate scrie, în funcţie de parametrii geometrici ai conului, folosind asemănarea semi-triunghiului de sub secţiune cu cel global:
![]()
Înlocuind aceste valori în ultimul rezultat de mai sus se face explicitarea lui σp(x) în funcţie de poziţia secţiunii:
![]()
Ultima expresie reprezintă grafic o porţiune de parabolă, având rădăcinile x=0 şi x=H, adică tensiunile circumferenţiale din pereţii vasului conic studiat sunt nule, la capetele înălţimii şi ating valoarea maximă la mijlocul vasului (ca în fig. 9.7), unde valoarea lor este:
![]()
Ecuaţia (9.2) se obţine folosind raţionamentele făcute anterior şi faptul că lichidul de sub secţiune ocupă un volum conic de rază r(x) şi înălţime x, inclus în ultimul termen din această ecuaţie:
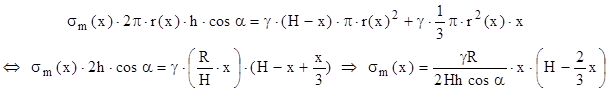
Tensiunile meridiane variază tot parabolic, dar au valori nule în x=0 şi într-o secţiune care este dincolo de limitele vasului, x=3H/2. Aceasta arată că se va atinge valoarea maximă (la jumătatea distanţei dintre rădăcini) în x=3H/4:
![]()
Deoarece se poate scrie 1/4=4/16, înseamnă că tensiunile cele mai mari sunt cele circumferenţiale, astfel încât condiţia de rezistenţă se scrie sub forma:
![]()
Concluzia acestei aplicaţii este că şi pentru vasele conice cu lichid, dacă nu au fost calculate corect, fisurarea tinde să apară pe direcţia generatoarei, mai precis în secţiunea de la jumătatea înălţimii vasului.